

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Ta thấy \(\widehat{AMN}=\widehat{ABH}+\frac{1}{2}\widehat{BHQ}=\widehat{ACH}+\frac{1}{2}\widehat{CHP}=\widehat{ANM}\). Suy ra \(\Delta AMN\) cân tại A.
b) Dễ thấy tứ giác BEFC và BQPC nội tiếp, suy ra \(\widehat{HEF}=\widehat{HCB}=\widehat{HPQ}\), suy ra EF || PQ
Hiển nhiên \(OA\perp PQ\). Do đó \(OA\perp EF.\)
c) Gọi MK cắt BH tại I, NK cắt CH tại J, HK cắt BC tại S.
Vì A,K là trung điểm hai cung MN của (AMN) nên AK là đường kính của (AMN)
Suy ra \(MK\perp AB,NK\perp AC\)hay MK || CH, NK || BH
Ta có \(\Delta BHQ~\Delta CHP\), theo định lí đường phân giác và Thales thì:
\(\frac{IH}{IB}=\frac{MQ}{MB}=\frac{NP}{NC}=\frac{JH}{JC}\). Suy ra IJ || BC
Cũng từ MK || CH, NK || BH suy ra HIKJ là hình bình hành hay HK chia đôi IJ
Do vậy HK chia đôi BC theo bổ đề hình thang. Vậy HK đi qua S cố định.

a, Xét tam giác vuông EBC vuông tại E và CI = IB
⇒ IE = IC = IB (1) ( vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
Xét tam giác vuông BCF vuông tại F và IC =IB
⇒IF = IC = IB (2) (vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
Từ (1) và (2) ta có:
IE = IF = IB = IC
Vậy bốn điểm B, C, E, F cùng thuộc một đường tròn tâm I bán kính bằng \(\dfrac{1}{2}\) BC (đpcm)
b, Xét \(\Delta\)AFC và \(\Delta\)AEB có:
\(\widehat{CAF}\) chung ; \(\widehat{AFC}\) = \(\widehat{AEB}\) = 900
⇒ \(\Delta\)AFC \(\sim\) \(\Delta\)AEB (g-g)
⇒ \(\dfrac{AF}{AE}\) = \(\dfrac{AC}{AB}\) (theo định nghĩa hai tam giác đồng dạng)
⇒AB.AF = AC.AE (đpcm)
Xét tam giác vuông AEH vuông tại E và KA = KH
⇒ KE = KH ( vì trong tam giác vuông trung tuyến ứng với cạnh huyền bằng \(\dfrac{1}{2}\) cạnh huyền)
⇒\(\Delta\)EKH cân tại K ⇒ \(\widehat{KEH}\) = \(\widehat{EHK}\)
\(\widehat{EHK}\) = \(\widehat{DHB}\) (vì hai góc đối đỉnh)
⇒ \(\widehat{KEH}\) = \(\widehat{DHB}\) ( tc bắc cầu) (3)
Theo (1) ta có: IE = IB ⇒ \(\Delta\) IEB cân tại I
⇒ \(\widehat{IEB}\) = \(\widehat{IBE}\) (4)
Cộng vế với vế của (3) và(4)
Ta có: \(\widehat{KEI}\) = \(\widehat{KEH}\) + \(\widehat{IEB}\) = \(\widehat{DHB}\) + \(\widehat{IBE}\) = \(\widehat{DHB}\) + \(\widehat{DBH}\)
Vì tam giác DHB vuông tại D nên \(\widehat{DHB}\) + \(\widehat{DBH}\) = 1800 - 900 = 900
⇒\(\widehat{KEI}\) = 900
IE \(\perp\) KE (đpcm)

Bài 2
a) Ta có \(\widehat{AEB}=\widehat{AHB}=90^o\). Tứ giác ABHE nội tiếp
=> \(\widehat{EHC}=\widehat{ABA'}=\widehat{BCA'}\)
=> HE//CA'
Vì CA' _|_ AC => HE _|_ AC
c) Gọi M là trung điểm của AB, N là trung điểm BC
Đường tròn ngoại tiếp ABHE có tâm là M nên M nằm trên đường trung trực của HE
Do HE _|_ AC nên trung trực của HE song song với AC và chứa đường trung bình của tam giác ABC
Do đó trung điểm N của BC nằm trên trung trự của HE
Mặt khác E,F là chân đường vuông góc của B và C hạ xuông AA' nên trung trực của EF đi qua trung điểm N của BC
Vậy N là tâm của đường tròn ngoại tiếp tam giác HEF là 1 điểm cố định cho BC cố định
Bài 1
bổ sung câu c bài hỏi .là : CM \(\frac{DE}{BE}=\frac{BD}{BA}\)
bài làm
a) ta có . tam giác ACO zuông tại C , Tam giác ABO zuông tại B
nên C , B lần lượt nhìn AO zới 1 góc =90 độ
=> ABCO nội tiếp
b) ta có tam giác ABC cân tại A do AB=AC
mà AH là đường cao
nên AH cx là đường trung tuyến
=> CH = HB
=> AO là đường trung trực của CB
c) ta có BD là đường kính của O
nên góc BED = 90 độ
xét 2 tam giác zuông BED zà ABD có
góc BAD = góc BDA ( cùng nhìn \(\widebat{BE}\)
BD chung
=> tam giác BED = tam giác DBA
=> \(\frac{DE}{BE}=\frac{BD}{BA}\)

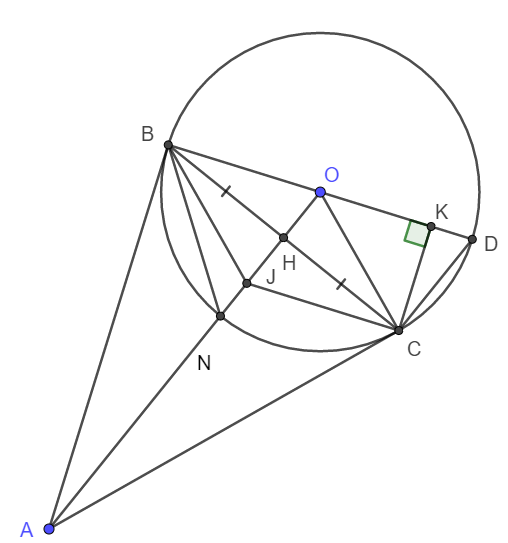
a) Tam giác vuông ABO và ACO có chung cạnh huyền AO nên O, B, A, C cùng thuộc đường tròn đường kính AO.
b) Theo tính chất hai tiếp tuyến cắt nhau, ta có AB = AC nên ABC là tam giác cân tại A.
Lại có AO là phân giác nên đồng thời là đường trung tuyến. Vậy thì AO đi qua H hay A, H, O thảng hàng.
Theo liên hệ giữa góc ở tâm và góc nội tiếp cùng chắn một cung, ta có \(\widehat{KDC}=\frac{\widehat{BOC}}{2}\)
Theo tính chất hai tiếp tuyến cắt nhau ta cũng có: \(\widehat{COA}=\frac{\widehat{BOC}}{2}\)
Suy ra \(\widehat{KDC}=\widehat{COA}\)
Vậy thì \(\Delta KDC\sim\Delta COA\left(g-g\right)\Rightarrow\frac{CK}{AC}=\frac{CD}{AO}\Rightarrow AC.CD=CK.AO\)
c) Ta thấy \(\widehat{ABN}=\widehat{NBC}\) (Góc nội tiếp và góc tạo bởi tiếp tuyến dây cung chắn các cung bằng nhau)
Vậy nên BN là phân giác góc ABC.
Lại có AN là phân giác góc BAC nên N là tâm đường tròn nội tiếp tam giác ABC.
d) Gọi J là trực tâm tam giác ABC. Ta có ngay \(JC\perp AB;BJ\perp AC\)
Vậy thì BO // JC ; BJ // OC
Suy ra tứ giác JBOC là hình bình hành.
Lại có OB = OC nên JBOC là hình thoi.
Từ đó ta có JB = JC = OB = OC = R.
Vậy khi A di chuyển trên tia By cố định thì BJ = R hay J thuộc đường tròn tâm B, bán kính R.

1: góc ADC=góc AEC=90 độ
=>ADEC nội tiếp
2: góc ABH=90 độ-góc BAC=góc DEA