Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

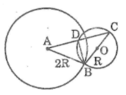
Tam giác BCD nội tiếp trong đường tròn (O) có BC là đường kính nên 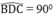
Suy ra : BD ⊥ AC (1)
Ta có : AB = 2R và BC = 2OB = 2R
Suy ra tam giác ABC cân tại B (2)
Từ (1) và (2) suy ra : AD = DC

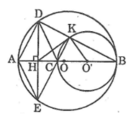
Vì O, O’ và B thẳng hàng nên: O’B < OB => O’ nằm giữa O và B
Ta có: OO’ = OB - O’B
Vậy đường tròn (O’) tiếp xúc với đường tròn (O) tại B

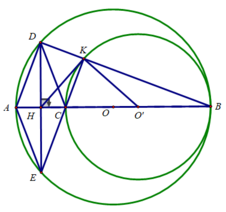
a) Ta có: OO' = OB – O'B
⇒ Hai đường tròn (O) và (O') tiếp xúc trong tại B

a: góc OBA+góc OCA=180 độ
=>OBAC nội tiếp
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC
góc DBC=1/2*180=90 độ
=>DB vuông góc bC
=>DB//OA
c: Xét ΔABE và ΔADB có
góc ABE=góc ADB
góc BAE chung
=>ΔABE đồng dạng với ΔADB
=>AB/AD=AE/AB
=>AB^2=AD*AE


Ta có: R < OA < 3R ⇔ 2R – R < OA < 2R + R
Suy ra hai đường tròn (O ; R) và (A ; 2R) cắt nhau