Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

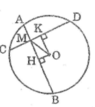
Ta có: HA = HB (gt)
Suy ra : OH ⊥ AB (đường kính dây cung)
Lại có : KC = KD (gt)
Suy ra : OK ⊥ CD (đường kính dây cung)
Mà AB > CD (gt)
Nên OK > OH (dây lớn hơn gần tâm hơn)
Áp dụng định lí Pitago vào tam giác vuông OHM ta có :
O M 2 = O H 2 + H M 2
Suy ra : H M 2 = O M 2 - O H 2 (1)
Áp dụng định lí Pitago vào tam giác vuông OKM ta có:
O M 2 = O K 2 + K M 2
Suy ra: K M 2 = O M 2 - O K 2 (2)
Mà OH < OK (cmt) (3)
Từ (1), (2) và (3) suy ra: H M 2 > K M 2 hay HM > KM

Bài tập 13 trang 106 SGK Toán 9 Tập 1 - H7.net
.png)
Câu a: Ta có:
AH=HB⇒OH⊥AB
KC=KD⇒OK⊥CD
Lại có:
AB=CD⇒OH=OK
⇒ΔHOE=ΔKOE(ch.cgv)
⇒EH=EK(1)
Câu b: Ta lại có:
AB=CD⇔AB2=CD2⇔AH=CK(2)
Từ (1) và (2):
⇒EH+HA=EK+KC⇔EA=EC
a. Ta có: HA = HB ( gt )
Suy ra : \(OH\perp AB\) ( đường kính dây cung )
Lại có : KC = KD ( gt )
Suy ra : \(OK\perp CD\)( đường kính dây cung )
Mà AB > CD ( gt )
Nên OK > OH ( dây lớn hơn gần tâm hơn )
Áp dụng định lí Pitago vào tam giác vuông OHM ta có :
OM2 = OH2 + HM2
Suy ra : HM2 = OM2 – OH2 (1)
Áp dụng định lí Pitago vào tam giác vuông OKM ta có:
OM2 = OK2 + KM2
Suy ra: KM2 = OM2 – OK2 (2)
Mà OH < OK ( cmt ) (3)
Từ (1) (2) và (3) suy ra: HM2 > KM2 hay HM > KM

a. Ta có: HA = HB (gt)
Suy ra : \(OH\perp AB\) (đường kính dây cung)
Lại có : KC = KD (gt)
Suy ra : \(OK\perp CD\) (đường kính dây cung)
Mà AB > CD (gt)
Nên OK > OH (dây lớn hơn gần tâm hơn)
Áp dụng định lí Pitago vào tam giác vuông OHM ta có :
OM2 = OH2 + HM2
Suy ra : HM2 = OM2 – OH2 (1)
Áp dụng định lí Pitago vào tam giác vuông OKM ta có:
OM2 = OK2 + KM2
Suy ra: KM2 = OM2 – OK2 (2)
Mà OH < OK (cmt) (3)
Từ (1), (2) và (3) suy ra: HM2 > KM2 hay HM > KM

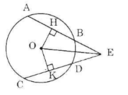
Nối OE ta có: AB = CD
=> OH = OK (Định lí 3)
Hai tam giác vuông OEH và OEK có:
OE là cạnh chung
OH = OK
=> ΔOEH = ΔOEK (cạnh huyền, cạnh góc vuông)
=> EH = EK (1). (đpcm)
