Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có
C A B ⏜ = 90 0 O H C ⏜ = 90 0 ⇒ C A B ⏜ + O H C ⏜ = 180 0
Vậy tứ giác AOHC nội tiếp.
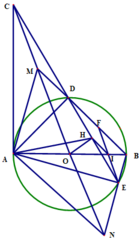
b) Ta có C A D ⏜ = A E C ⏜ , A C E ⏜ chung suy ra Δ A C D ~ Δ E C A (g.g)
⇒ C A C E = A D A E ⇒ A C . A E = A D . C E
c) Từ E vẽ đường thẳng song song với MN cắt cạnh AB tại I và cắt cạnh BD tại F ⇒ H E I ⏜ = H C O ⏜ .
Vì tứ giác AOHC nội tiếp ⇒ H A O ⏜ = H C O ⏜ = H E I ⏜ .
Suy ra tứ giác AHIE nội tiếp ⇒ I H E ⏜ = I A E ⏜ = B D E ⏜ ⇒ H I / / B D .
Mà H là trung điểm của DE=> I là trung điểm của EF. Có EF//MN và IE= IF
=> O là trung điểm của đoạn thẳng MN.
Suy ra tứ giác AMBN là hình bình hành => AM//BN.

Cho đường tròn tâm O có đường kính AB R2 . Gọi M là điểm di động trên đường tròn O . Điểm M khác AB, ; dựng đường tròn tâm M tiếp xúc với AB tại H . Từ A và B kẻ hai tiếp tuyến AC và BD với đường tròn tâm M vừa dựng.
a) Chứng minh BM AM , lần lượt là các tia phân giác của các góc ABD và BAC .
b) Chứng minh ba điểm C M D , , nằm trên tiếp tuyến của đường tròn tâm O tại điểm M .
c) Chứng minh AC BD không đổi, từ đó tính tích AC BD. theo CD .
d) Giả sử ngoài AB, trên nửa đường tròn đường kính AB không chứa M có một điểm N cố định. gọi I là trung điểm của MN , kẻ IP vuông góc với MB . Khi M chuyển động thì P chuyển động trên đường cố định nào.
Cần giải câu d

Bài 4:
a:
Xét (O) có
ΔCED nội tiếp
CD là đường kính
=>ΔCED vuông tại E
ΔOEF cân tại O
mà OI là đường cao
nên I là trung điểm của EF
Xét tứ giác CEMF có
I là trung điểm chung của CM và EF
CM vuông góc EF
=>CEMF là hình thoi
=>CE//MF
=<MF vuông góc ED(1)
Xét (O') có
ΔMPD nội tiêp
MD là đường kính
=>ΔMPD vuông tại P
=>MP vuông góc ED(2)
Từ (1), (2) suy ra F,M,P thẳng hàng
b: góc IPO'=góc IPM+góc O'PM
=góc IEM+góc O'MP
=góc IEM+góc FMI=90 độ
=>IP là tiếp tuyến của (O')

a, ta có: góc AEI = 90o (góc nội tiếp chắn nửa đường tròn) => EI\(\perp\)AK tại E và AH\(\perp\)KI tại H (gt)
chúng cắt nhau tại B => B là trực tâm. => KB vuông góc AI (đpm)
b, ta có: góc ECA = góc EBA ( cùng chắn cung AE) mà góc EBA= góc HBI (hai góc đối đỉnh) (4)
ta lại có: góc HBI + góc HIB =90o (tổng 3 góc trong một tam giác) (3)
=> góc ECA + góc HIB = 90o (1)
Xét tam giác CEI vuông tại E nên: góc EKI + góc HIB =90o (2)
Từ (1) và (2) => góc ECA = góc EKI
=> tứ giác EKNC là tứ giác nội tiếp ) (đpcm)
c,Ta có: góc EAB + góc EBA = 90o và từ (3), (4) => góc EAB = góc BIH
mà góc EAB = góc BEN ( bằng 1/2 sđ cung EB)
=> góc BIH = góc BEN=> tam giác ENI cân tại N=> EN =NI (*)
Tương tự, ta có góc K + góc KAH = 90o
góc KEN + góc NEB =90o mà góc KAH = góc NEB (c.m.t) => góc KEN = góc K => tam giác KNE cân tại N => NK = NE (**)
từ (*) và (**) => NK = NI hay N là trung điểm KI ( đpcm)
