Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C
b: Xét ΔABC vuông tại C có CH là đường cao
nên \(AH\cdot AB=AC^2\left(1\right)\)
Xét ΔMAB vuông tại A có AC là đường cao
nên \(MC\cdot BC=AC^2\left(2\right)\)
Từ (1) và (2) suy ra \(AH\cdot AB=MC\cdot BC\)

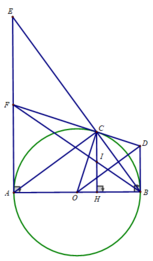
b) DC và DB là 2 tiếp tuyến cắt nhau tại D
⇒ DC = DB
Lại có: OC = OB = R
⇒ OD là đường trung trực của BC hay OD ⊥ BC

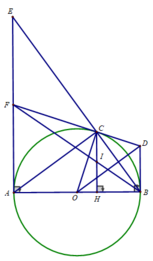
d) Xét tam giác ACB vuông tại C, CH là đường cao nên :
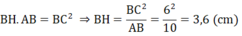
Xét tam giác ABE vuông tại A, AC là đường cao nên :

⇒ EA = 2 FA ⇒ F là trung điểm của EA
Tam giác CEA vuông tại C có CF là trung tuyến
⇒ FC = FA
⇒ ΔFCA cân tại F ⇒ ∠(FCA) = ∠(FAC)
Lại có ΔOCA cân tại O ⇒ ∠(OCA) = ∠(OAC)
⇒ ∠(FCA) + ∠(OCA) = ∠(FAC) + ∠(OAC)
⇔ ∠(FCO) = ∠(FAO) = 90 0
Vậy FC ⊥ CO hay FC là tiếp tuyến của (O)

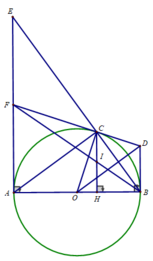
c) Xét tam giác ACB vuông tại C, CH là đường cao nên :
AH.AB = A C 2
Xét tam giác ABE vuông tại A, AC là đường cao nên :
EC.BC = A C 2
⇒ AH.AB = EC.BC
a) Tam giác ABC nội tiếp (O) có AB là đường kính
⇒ ∠(ACB) = 90o
Hay tam giác ABC vuông tại C
Tam giác ABC vuông tại C, CH là đường cao có: