Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

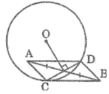
Ta có: OI ⊥ CD (gt)
Suy ra: IC = ID (đường kính dây cung)
Mà: IA = IB (gt)
Tứ giác ACBD có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành.

Lời giải:
Đề bài cần bổ sung OA cắt (O) tại E sao cho E nằm giữa O và A.
Do $AB$ là tiếp tuyến $(O)$ nên $AB\perp OB$ hay tam giác $ABO$ vuông tại $B$. Mà $AB=2BO$ (do $AB=2R; BO=R$). Do đó $\widehat{BOA}=60^0$
Tam giác $BOE$ có $BO=EO=R$ nên là tam giác cân. Mà $\widehat{BOE}=\widehat{BOA}=60^0$ nên $BOE$ là tam giác đều.
$\Rightarrow BO=BE(1)$$OB=OC$ và $OA\perp BC$ nên $OA$ là đường trung trực của $BC$
$E\in OA$ nên $EB=EC(2)$
$OB=OC=R(3)$
Từ $(1);(2);(3)\Rightarrow OC=BO=BE=EC$. Suy ra OBEC là hình thoi.

Bài 1:
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay ΔMAB cân tại M
mà \(\widehat{AMB}=60^0\)
nên ΔMBA đều
b: Xét ΔAOM vuông tại A có
\(AM=OA\cdot\tan30^0\)
nên \(AM=5\sqrt{3}\left(cm\right)\)
\(C_{AMB}=3\cdot AM=15\sqrt{3}\left(cm\right)\)
c: Ta có: MA=MB
nên M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
hay MO⊥AB(1)
Xét (O) có
ΔABC nội tiếp
AC là đường kính
DO đó: ΔABC vuông tại B
Suy ra: AB⊥BC(2)
Từ (1) và (2) suy ra OM//BC
hay BMOC là hình thang

c
Gọi H là giao điểm của AB và OM
a, Xét Δv MAO và ΔvMBO
Có MO chung
AO=OB(=bk)
=> ΔvMAO= ΔMBO (ch-cgv)
=> MA=MB
Trong ΔAMB
Có MA=MB(cmt)
=> ΔAMB cân tại M
lại có góc AMB=60 độ
=> ΔAMB là Δ đều
b, Ta có: góc AMO=góc BMO ( ΔvMAO= ΔvMBO)
mà góc AMO+ góc BMO= góc AMB=60 độ
=> góc AMO=\(\frac{1}{2}.60=30^0\)
Áp dụng tỉ số lượng giác
Ta có : tan góc AMO=\(\frac{AO}{AM}\)
tan30=\(\frac{5}{AM}\)
=>AM=\(\frac{5}{tan30}=5\sqrt{3}\)
Chu vi ΔAMB= AM.3=\(5\sqrt{3}.3=15\sqrt{3}\)
c, Ta có OA=OB (=bk)
=> O thuộc đường trung trực AB(1)
MA=MB(cmt)
=> M thuộc đường trung trực AB (2)
Từ (1)(2)=> OM là cả đường trung trực
=> MO vuông góc AB (*)
Ta có: OA=OB=OC(=bk)
=> OB=\(\frac{1}{2}AC\)
mà OB là đường trung tuyến
=> Δ ABC vuông tại B
=> AB vuông góc BC(**)
Từ (*)(**)=> MO//BC
=> BMOC là hình thang
Bài 2:
a,
Ta có : góc AQM=90 độ ( MQ vuông góc xy)
góc APM =90 độ ( MP vuông góc AB)
góc QAP=90độ ( xy vuông góc OA)
=> QMPA là hình chữ nhật
b, Trong hình chữ nhật QMPA:
Có : I là trung điểm của đường chéo thứ nhất QP
-> I cũng là trung điểm của đường chéo thứ 2 AM
=> IA=IM
=> OI vuông góc AM tại I ( đường kính đi qua trung điểm => vuông góc ( đ/Lý 3)

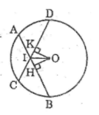
Kẻ OH ⊥ AB, OK ⊥ CD
Ta có: AB = CD (gt)
Suy ra : OH = OK (hai dây bằng nhau cách đều tâm)
Vậy OI là tia phân giác của góc BID (tính chất đường phân giác)


