Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường tròn (C): x 2 + y 2 + 6 x − 2 y − 8 = 0 có tâm I(-3;1) và bán kính R = 3 2 .
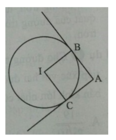
Giả sử hai tiếp điểm của hai tiếp tuyến kẻ từ A là B, C (như hình vẽ).
Tứ giác IBAC có 3 góc vuông nên là hình chữ nhật.
Lại có IB = IC = R nên IBAC là hình vuông. Suy ra, tam giác IBA vuông cân.
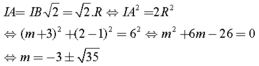
Chọn A

Qua điểm A(m ; m + 2) có hai tiếp tuyến với (C) khi và chỉ khi A nằm ngoài (C)
⟺ m 2 + m + 2 2 + 4 m − 2 m − 4 > 0 ⇒ 2 m 2 + 6 m > 0 ⇒ m > 0 m < − 3
Chọn D

Qua điểm A(-1; m) chỉ có một tiếp tuyến với (C) khi và chỉ khi A ∈ ( C
⟺1+ m 2 − 3 − 5 m + 8 = 0
m 2 − 5 m + 6 = 0 ⇒ m = 2 , m = 3
Chọn B

a, Phương trình tiếp tuyến đi qua M: \(ax+by-3a+b=0\left(\Delta\right)\)
Đường tròn đã cho có tâm \(I=\left(1;-2\right)\) bán kính \(R=\sqrt{5}\)
Ta có: \(d\left(I;\Delta\right)=\dfrac{\left|a-2b-3a+b\right|}{\sqrt{a^2+b^2}}=\sqrt{5}\)
\(\Leftrightarrow\left(2a+b\right)^2=5\left(a^2+b^2\right)\)
\(\Leftrightarrow\left(a-2b\right)^2=0\)
\(\Leftrightarrow a=2b\)
\(\Rightarrow\Delta:2x+y-5=0\)
b, Phương trình tiếp tuyến: \(\left(d\right)2x-y+m=0\left(m\in R\right)\)
Ta có: \(d\left(I;d\right)=\dfrac{\left|2.1-1.\left(-2\right)+m\right|}{\sqrt{5}}=\sqrt{5}\)
\(\Leftrightarrow\left|m+4\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\\m=-9\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}d:2x-y+1=0\\d:2x-y-9=0\end{matrix}\right.\)

Đường tròn (C) tâm \(I\left(-2;-1\right)\) bán kính \(R=1\)
\(\overrightarrow{IM}=\left(m+2;3-m\right)\Rightarrow IM^2=\left(m+2\right)^2+\left(3-m\right)^2=2m^2-2m+13\)
Giả sử A nằm ngoài đường tròn và 2 tiếp điểm là B và C
\(\Rightarrow\widehat{BAC}=60^0\Rightarrow\widehat{IAB}=30^0\)
\(\Rightarrow IM=\frac{IB}{sin30^0}=2IB=2R=2\Rightarrow IM^2=4\)
\(\Rightarrow2m^2-2m+13=4\Leftrightarrow2m^2-2m+9=0\) (vô nghiệm)
Ko tồn tại m thỏa mãn
Bạn xem lại đề, điểm M nằm quá xa đường tròn (M thuộc \(x+y-2=0\) ) nên góc chắc chắn là rất nhỏ

Đường tròn (C): x 2 + y 2 + 4 x + 2 y + 4 = 0 có tâm I(-2;-1) và bán kính R = 1.
Gọi 2 tiếp điểm là B và C.
Ta có: B A C ^ = 60 0 nên B A I ^ = I A C ^ = 1 2 B A C ^ = 30 0 ( tính chất 2 tiếp tuyến cắt nhau).
Vì sin B A I ^ = sin 30 0 = 1 2 ; lại có: sin B A I ^ = B I A I = R A I
Suy ra: R A I = 1 2 ⇔ A I = 2 R = 2 ( vì R = 1)
⇔ m + 2 2 + 3 − m 2 = 2 2 ⇒ 2 m 2 − 2 m + 9 = 0 (vô nghiệm).
Chọn D.