Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử C là giao điểm của đoạn thẳng AB với đường thẳng d.
Vì C nằm giữa A và B nên ta có:
AC + CB = AB (1)
Lấy điểm C' bất kỳ trên d (C' ≠ C)
Nối AC', BC'
Sử dụng bất đẳng thức trong tam giác vào ∆ABC', ta có:
AC' + BC' > AB (2)
Từ (1) và (2) suy ra:
AC' + C'B > AC + CB.
Vậy điểm C cần tìm là giao điểm của đường thẳng AB với đường thẳng d.

* Phân tích
Giả sử điểm M thuộc xy đã tìm được để có MA+ MB là ngắn nhất.
Lấy A’ đối xứng với A qua xy
ta có: MA = MA’
suy ra MA’ + MB cũng ngắn nhất .
Mà A và B lại nằm trên hai nửa mặt phẳng đối nhau có bờ là đường thẳng xy
Nên M phải nằm giữa A’và B tức là MA’ + MB = A’B
Suy ra M phải là giao của A’B và xy.
* Cách dựng
Dựng A’ đối xứng với A qua xy,
Nối A’với B cắt xy tại điểm M
*Chứng minh :
Nối M với A ta có MA = MA’ (A và A’ đối xứng với nhau qua xy)
Mà MA’ + MB = A’B
suy ra MA+MB =A’B là ngắn nhất
Thật vậy: nếu lấy một điểm M’ thuộc xy mà M’ khác M ,
nối M’ với A’ và M’ với B
ta có tam giác M’A’B.
Do đó M’A’ + M’B > A’B
mà M’A’ = M’A’(tính chất đối xứng).

- Tìm điểm A’ đối xứng với A qua d
- Nối A’B cắt d tại M . M chính là điểm cần tìm .
- Thật vậy : Vì A’ đối xứng với A qua d cho nên MA=MA’ (1). Do đó :
MA+MB=MA’+MB=A’B .
- Giả sử tồn tại M’ khác M thuộc d thì : M’A+M’B=M’A’+M’B
'A B≥
. Dấu bằng chỉ
xảy ra khi A’M’B thẳng hàng . Nghĩa là M trùng với M’

Lấy D là điểm đối xứng, với A qua d. Theo tính chất đường trung trực: CA = CD.
Do đó CA + CB = CD + CB.
Gọi M là giao điểm của BD và d.
Nếu C không trùng với M thì xét tam giác BCD, ta có: CB + CD > BD hay CA + CB > BD (1).
Nếu C trùng với M thì:
CA + CB = MA + MB = MD + MB = BD (2).
So sánh (1) và (2) ta thấy điểm C trùng M hay C là giao điểm của BD và d thì giá trị của tổng CA + CB là nhỏ nhất.
Chú ý: Điểm C tìm được ở vị trí M như vậy là điểm duy nhất. Thật vậy, nếu lấy E đối xứng với B qua d thì AE vẫn cắt d ở M đúng vị trí mà BD cắt d.
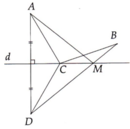

C là giao của AB với d thì tổng AC+CB là nhỏ nhất vì
Nếu C không thuộc AB thì 3 điểm A,B,C sẽ tạo thành 1 tam giác
Trong tam giác ABC thì AC+CB>AB (Trong tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại)
=> AC+CB nhỏ nhất khi =AB tức là C thuộc AB
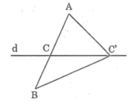
- Tìm điểm A’ đối xứng với A qua d
- Nối A’B cắt d tại M . M chính là điểm cần tìm .
- Thật vậy : Vì A’ đối xứng với A qua d cho nên MA=MA’ (1). Do đó :
MA+MB=MA’+MB=A’B .
- Giả sử tồn tại M’ khác M thuộc d thì : M’A+M’B=M’A’+M’B
'A B≥
. Dấu bằng chỉ
xảy ra khi A’M’B thẳng hàng . Nghĩa là M trùng với M’
- Tìm điểm A’ đối xứng với A qua d
- Nối A’B cắt d tại M . M chính là điểm cần tìm .
- Thật vậy : Vì A’ đối xứng với A qua d cho nên MA=MA’ (1). Do đó :
MA+MB=MA’+MB=A’B .
- Giả sử tồn tại M’ khác M thuộc d thì : M’A+M’B=M’A’+M’B
'A B≥
. Dấu bằng chỉ
xảy ra khi A’M’B thẳng hàng . Nghĩa là M trùng với M’