
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



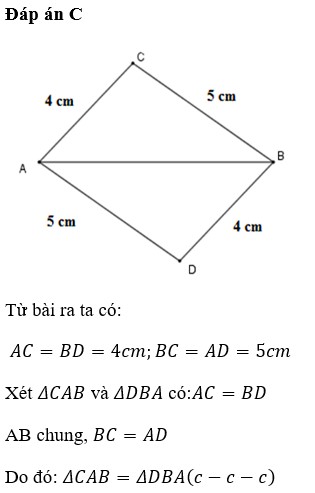
a: Xét ΔABM và ΔACM có
AB=AC
AM chug
BM=CM
Do đó: ΔABM=ΔACM
b:
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
Xét ΔAMC vuông tại M và ΔBMD vuông tại M có
MC=MD
MA=MB
Do đó: ΔAMC=ΔBMD
Suy ra: AC=BD
c: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của CB
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
d: Xét tứ giác ABCI có
AI//BC
AI=BC
Do đó: ABCI là hình bình hành
Suy ra: CI//AB
mà CD//AB
và CI,CD có điểm chung là C
nên C,I,D thẳng hàng

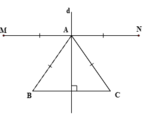
Ta có: B A M ^ = B ^ ( g t ) C A N ^ = C ^ ( g t )
Þ AM // BC; AN // BC (vì có cặp góc so le trong bằng nhau).
Þ 3 điểm M, A, N thẳng hàng (vì qua điểm A chỉ vẽ được một đường thẳng song song với BC).
Vậy MN // BC mà d ⊥ B C nên d ⊥ M N (1)
Ta có: A M = A B ; A N = A C
mà AB = AC (gt) nên AM = AN. (2)
Từ (1) và (2) Þ d là trung trực của MN

a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD