Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo hình vẽ taco:
AC=BC,MA=MB ( giả thiết )
MC chung
=> ΔAMC = Δ BMC ( c.c.c)
=> góc M1 = góc M2
Nhưng Góc M1 + M2 = 180 độ
nên: M1 =M2 = 90 độ
Do đó CM vuông góc vs AB

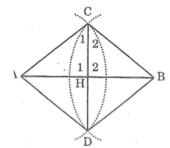
Gọi H là giao điểm của AB và CD
Nối AC, AD,BC,BD
Xét ΔACD và ΔBCD, ta có:
AC = BC
(bán kính hai cung tròn bằng nhau)
AD = BD
CD cạnh chung
Suy ra: ΔACD = ΔBCD(c.c.c)
Suy ra: ∠C1 = ∠C2 (hai góc tương ứng)
Xét hai tam giác AHC và BHC. Ta có:
AC = BC (bán kính hai cung tròn bằng nhau)
∠C1 = ∠C2 (chứng minh trên)
CH cạnh chung
Suy ra: ΔAHC = ΔBHC(c.g.c)
Suy ra: AH = BH (hai cạnh tương ứng) (1)
Ta có : ∠H1 = ∠H2 (hai góc tương ứng)
∠H1 + ∠H2 =180° (hai góc kề bù)
Suy ra: ∠H1 = ∠H2 = 90o ⇒ CD ⊥ AB (2)
Từ (1) và (2) suy ra CD là đường trung trực của AB

Bạn chỉ cần viết lại khúc từ cung tròn tâm A đến ở C và D rồi suy ra AC=AB=AD=BD=BC là đc nhé còn lại tự giải

Xét hai tam giác ACD và BCD có:
AC = BC (gt)
AD = BD (gt)
CD: cạnh chung
Vậy: \(\Delta ACD=\Delta BCD\left(c-c-c\right)\)
Suy ra: \(\widehat{C_1}=\widehat{C_2}\) (hai góc tương ứng)
Xét hai tam giác ACH và BCH có:
AC = BC (gt)
\(\widehat{C_1}=\widehat{C_2}\) (cmt)
CH: cạnh chung
Vậy: \(\Delta ACH=\Delta BCH\left(c-g-c\right)\)
Suy ra: \(\widehat{H_1}=\widehat{H_2}\), HA = HB
Mà \(\widehat{H_1}+\widehat{H_2}=180^o\)
Nên \(\widehat{H_1}=\widehat{H_2}\) = 90o
Do đó: \(CH\perp AB\)
Vì \(CD\perp AB\)và HA = HB nên CD là đường trung trực của AB.
ta có : mình vẽ ko đúng lắm nhé
xét tam giác acm và tam giác bcm
có:am=bm(cùng bằng bán kính)
chung cm
bc=ca(m là trung điểm của ab)
vậy tam giac acm băng tam giác bcm (c.c.c)
vậy góc cma=góc cmb(2 góc tương ứng)
vì acb=180o mà cm nằm giữa ca và cb
vậy góc cma= góc cmb=góc acb/2=1800/2=90o
vậy góc cma và cmb vuông
vậy cm vuông góc với ab