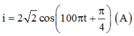Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn nên gửi mỗi câu hỏi một bài thôi để mọi người tiện trao đổi.
1. \(Z_L=200\sqrt{3}\Omega\), \(Z_C=100\sqrt{3}\Omega\)
Suy ra biểu thức của i: \(i=1,1\sqrt{2}\cos\left(100\pi t-\frac{\pi}{3}\right)A\)
Công suất tức thời: p = u.i
Để điện áp sinh công dương thì p > 0, suy ra u và i cùng dấu.
Biểu diễn vị trí tương đối của u và i bằng véc tơ quay ta có:
Như vậy, trong 1 chu kì, để u, i cùng dấu thì véc tơ u phải quét 2 góc như hình vẽ.
Tổng góc quét: 2.120 = 2400
Thời gian: \(t=\frac{240}{360}.T=\frac{2}{3}.\frac{2\pi}{100\pi}=\frac{1}{75}s\)
2. Khi nối tắt 2 đầu tụ điện thì cường độ dòng điện hiệu dụng không đổi \(\Rightarrow Z_1=Z_2\Leftrightarrow Z_C-Z_L=Z_L\Leftrightarrow Z_C=2Z_L\)
\(U_C=1,2U_d\Leftrightarrow Z_C=2Z_d\Leftrightarrow Z_C=2\sqrt{R^2+Z_L^2}\)
\(\Leftrightarrow2Z_L=\sqrt{R^2+Z_L^2}\Leftrightarrow R=\sqrt{3}Z_L\)
Khi bỏ tụ C thì cường độ dòng điện của mạch là: \(I=\frac{U}{Z_d}=\frac{U}{\sqrt{R^2+Z_L^2}}=\frac{220}{\sqrt{3.Z_L^2+Z_L^2}}=0,5\)
\(\Rightarrow Z_L=220\Omega\)

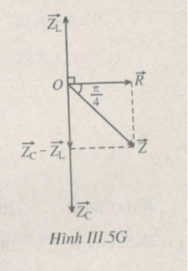
Xem giản đồ Fre-nen (H.III.5G)
Z L = ω L = 100 π .1/10 π = 100 Ω
Z C = 1/ ω C = 20 Ω
![]()
U = U L 2 = 20 2
⇒ u = 40cos(100 π t - π /4)

Giải thích: Đáp án D
+ Từ biểu thức của i1 và i2 ta có: ![]()
+ Độ lệch pha giữa điện áp và cường độ dòng điện trong mạch RL và RC:
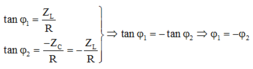
+ Ta lại có: 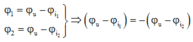
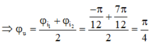
+ Xét mạch RL: 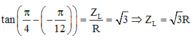
Tổng trở và dòng điện trong mạch khi đó:
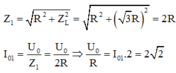
+ Nếu đặt điện áp trên vào hai đầu đoạn mạch RLC nối tiếp thì
![]()
Cường độ dòng điện cực đại trong mạch: ![]()
Do ZL = ZC nên trong mạch có cộng hưởng, khi đó: ![]()
Cường độ dòng điện trong mạch: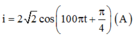

\(Z_L=\omega L=10\Omega\)
\(Z_C=\frac{1}{\omega C}=20\Omega\)
Ta có giản đồ véc tơ
Ta có: \(U_L=U_R=\frac{U_C}{2}\)
Từ giản đồ véc tơ ta có:
\(U_0=U_{0L}\sqrt{2}=20\sqrt{2}\sqrt{2}=40V\)
u trễ pha \(\frac{3\pi}{4}\) với uL
\(\Rightarrow u=40\cos\left(100\pi t+\frac{\pi}{2}-\frac{3\pi}{4}\right)\)
\(\Rightarrow u=40\cos\left(100\pi t-\frac{\pi}{4}\right)\)(V)
Chọn B.
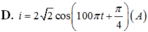

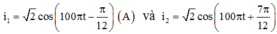 (A).
(A).