Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là D.
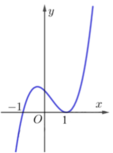
Để đường thẳng y = 2 m - 1 cắt ( C ) tại hai điểm phân biệt thì 2 m - 1 = 5 2 m - 1 = 1 ⇔ m = 3 m = 1

Đáp án B
Lấy đối xứng đồ thị hàm số f(x)(x-1) qua trục Ox ta được đồ thị của hàm số f x x - 1 . Từ đồ thị hàm số f x x - 1 ta thấy đường thẳng y = m 2 - m cắt hàm số f x x - 1 tại 2 điểm nằm ngoài [-1;1]
⇔ m 2 - m > 0 ⇔ [ m < 0 m > 1

Đáp án C
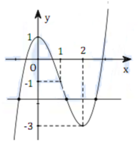
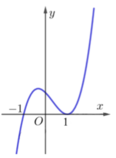
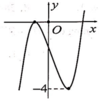
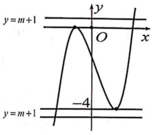
Em có f(1) = -1. Do đường thẳng y = m +1 có đồ thị là một đường thẳng song song hoặc trùng với trục hoành. Vậy để đường thẳng y = m +1 cắt (C) tại ba điểm phân biệt có hoành độ x 1 < 1 < x 2 < x 3 thì đường thẳng y = m +1 phải cắt đồ thị như hình vẽ
⇔ − 3 < m + 1 < − 1 ⇔ − 4 < m < − 2

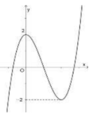
Đáp án B
Lấy đối xứng đồ thị hàm số f ( x ) ( x − 1 ) qua trục Ox ta được đồ thị của hàm số f ( x ) x − 1 . Từ đồ thị hàm số f ( x ) x − 1 ta thấy đường thẳng y = m 2 − m cắt hàm số f ( x ) x − 1 tại 2 điểm nằm ngoài [ − 1 ; 1 ] ⇔ m 2 − m > 0 ⇔ m < 0 m > 1
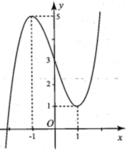
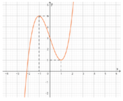






Đáp án C.
Đồ thị hàm số y = f x C 1 được suy ra từ đồ thị của hàm số y = f x C như sau:
+ Hàm số y = f x là hàm chẵn có đồ thị đối xứng qua trục tung
+ Hàm số y = f x = f x , x ≥ 0 − f x , x < 0
+ Đồ thị hàm số y = f x gồm hai phần
Phần 1: Là đồ thị (C) ở bên phải trục Oy
Phần 2: Đối xứng của phần 1 qua Oy
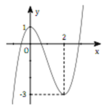
+ Vẽ đồ thị C 1 như hình vẽ
Để đường thẳng y = 2m cắt C 1 tại 4 điểm phân biệt khi − 2 < 2 m < 2 ⇔ − 1 < m < 1