Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

M cách đều Ox và Oy nên M nằm trên tia phân giác của góc xOy.
Gọi A là chân đường vuông góc kẻ từ M đến Ox thì tam giác vuông AOM là một nửa tam giác đều.
Do đó, OM = 2MA = 12cm.

Gọi K, H lần lượt là hình chiếu của M lên Ox, Oy
Ta có: MH=MK=5cm
Xét 2 tam giác vuông HOM và tam giác KOM có:
MH=MK
OM chung
=> tam giác HOM=KOM ( cạnh huyền cạnh góc vuông)
=> \(\widehat{HOM}=\widehat{KOM}=\frac{1}{2}.60^o=30^o\)
Sử dụng bổ đề: Trong môt tam giác vuông độ dài cạnh huyền bằng 2 lần độ dài cạnh góc vuông đối diện với góc 30 độ
Xét tam giác HOM vuông tại H có OM là cạnh huyền, \(\widehat{HOM}=30^o\)
=> OM=2.HM=2.5=10 (cm)

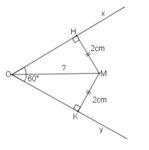
M cách đều Ox và Oy
⇒ M thuộc tia phân giác của góc xOy.
⇒ ∠MOx = 30o
∆MHO vuông có cạnh HM đối diện với góc HOM
*) Áp dụng bài 6.5 ( sách bài tập – tập 1): Nếu tam giác ABC vuông tại A và ∠B = 30o
thì AC= BC/2
⇒ HM = 1/2.OM
⇒ OM = 2.HM = 2.2 = 4 (cm)
Chọn đáp án: C

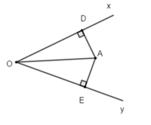
Điểm A nằm trong góc xOy và cách đều hai tia Ox và Oy, do đó A nằm trên tia phân giác của góc xOy hay OA là tia phân giác của góc xOy
⇒ x O A ^ = 1 2 x O y ^ = 1 2 .60 ° = 30 °
Gọi D và E lần lượt là chân đường vuông góc của A lên Ox và Oy
Khi đó AD = AE = 6 cm; D O A ^ = 30 °
Trong tam giác AOD vuông ở D có D O A ^ = 30 °
Suy ra AD = 1 2 OA (Trong tam giác vuông cạnh đối diện với góc 30 ° bằng một nửa cạnh huyền).
O A = 2 A D = 2.6 = 12 c m
Chọn đáp án D

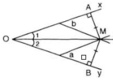
(Từ bài tập 12 ta biết rằng: độ dài đường vuông góc giữa hai đường thẳng song song chính là khoảng cách giữa hai đường thẳng đó.)
Gọi A, B lần lượt là chân đường cao hạ từ M xuống Ox, Oy ⇒ MA, MB lần lượt là khoảng cách từ M đến Ox, Oy.
Theo cách vẽ bằng thước hai lề và từ bài tập 12 ta suy ra: MA = MB (cùng bằng khoảng cách hai lề của thước) hay điểm M cách đều hai cạnh của góc xOy.
Áp dụng định lý 2 suy ra: OM là tia phân giác của góc xOy.
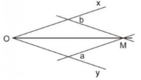
.Khi đó đoạn OM bằng 4cm