Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lớn rồi có ý thức chút đi buff sp bị người khác phát hiện mà cứ cố cãi làm gì
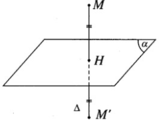
Phương trình tham số của đường thẳng ∆ đi qua điểm M(1; -1; 2) và vuông góc với mặt phẳng ( α ): 2x – y + 2z + 12 = 0 là:
Δ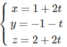 
Xét điểm H(1 + 2t; -1 – t; 2 + 2t) ∈ ∆
Ta có H ∈ ( α ) ⇔ 2(1 + 2t) + (1 + t) + 2(2 + 2t) + 12 = 0 ⇔ t = −19/9
Vậy ta được 
Vecto pháp tuyến của mp α là n → =(2;-1;2), H là hình chiếu vuông góc của M trên mp α nên M H ⊥ m p α , đường thẳng MK có vecto pháp tuyến n → = ( 2 ; - 1 ; 2 )
Ta có pt tham số của đường thẳng MH là : x = 1 + 2 t y = - 1 - t z = 2 + 2 t
Thay x,y,z từ pt tham số của đường thẳng MH và pt mp α , ta có:
2(1+2t)-(-1-t)+2(2+2t)+11=0 <=> t=-2
Vậy H(-3;1;-2)
M’ đối xứng với M qua (α)
⇒ H là trung điểm MM’
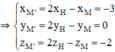
⇒ M’(-3; 0; -2).
Đáp án B
Phương pháp giải: Viết phương trình đường thẳng vuông góc với mặt và đi qua điểm, tọa độ giao điểm của đường thẳng và mặt phẳng chính là tọa độ hình chiếu của điểm
Lời giải:
Gọi H là hình chiếu của A trên α
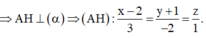
=> t= - 1
Vậy tọa độ điểm cần tìm là H(-1;1;-1)
Chọn A
Gọi 
là một vec tơ pháp tuyến của mặt phẳng (P).
Theo đề bài ta có mặt phẳng (P) vuông góc với mặt phẳng (α): x-y+z-4=0 nên ta có phương trình a-b+c=0 ó b=a+c 
Phương trình mặt phẳng (P) đi qua A(0;1;2) và có véc tơ pháp tuyến là ax+ (a+c) (y-1)+c (z-2) =0
Khoảng cách từ tâm I (3;1;2) đến mặt phẳng (P) là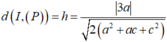 
Gọi r là bán kính của đường tròn giao tuyến giữa mặt cầu (S) và mặt phẳng (P) ta có r²=16-h² ; r nhỏ nhất khi h lớn nhất.
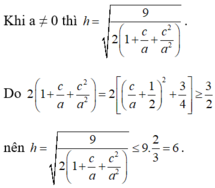
Dấu “=” xảy ra khi a = -2c. => một véc tơ pháp tuyến là 
=> phương trình mặt phẳng (P) là 2x+y-z+1=0.
Vậy tọa độ giao điểm M của (P) và trục x'Ox là: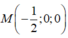 
Đường thẳng MH vuông góc với (α)
⇒ MH nhận vtpt của (α)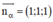
là 1 vtcp
Mà M(1; 4; 2) ∈ MH
⇒ Pt đường thẳng MH: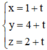
⇒ H(1 + t; 4 + t; 2 + t).
H ∈ (α) ⇒ 1 + t + 4 + t + 2 + t – 1 = 0 ⇔ t = -2.
⇒ H(-1; 2; 0).