Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cái này chưa có ai trả lời hả ? ai có câu trả lời ko giúp mik vs ạ mik cần rất gấp cảm ơn m.n

Cô hướng dẫn nhé :)
a. Tứ giác AOBM nội tiếp đường tròn đường kính OM. Tứ giác AHIM nội tiếp đường tròn đường kính AM.
b. Ta thấy góc NAM = góc AQN (Cùng chắn góc AN)
Vậy \(\Delta AMN\sim\Delta QMA\left(g-g\right)\)
Từ đó \(\frac{AM}{QM}=\frac{MN}{AM}\Rightarrow AM^2=MN.QM\)
c. Ta thấy NA = NB nên góc NAB = góc NBA. Lại có góc NAB = góc MBN (cùng chắn NB) nên BK là phân giác góc ABM. Nếu K là trung điểm AM thì tam giác cân AMB trở thành tam giác đều. Từ đó BK vuông góc AM hay N là trực tâm. Do AI vuông góc BM nên AI đi qua N hay A, N, I thẳng hàng.
Chúc em học tốt :)


( mấy cái cơ bản thì tự viết nhé )
a) góc MAO và góc MBO= 90 độ
xét tứ giác MAOB có góc MAO+MBO=180 độ
=> MAOB nội tiếp
b) Xét (O) có EB là tiếp tuyến của (O)
\(\Rightarrow\widehat{EBD}=\widehat{EAB}\left(=\frac{1}{2}sđ\widebat{DB}\right)\)
Xét tam giác EDB và tam giác EBA có:
\(\hept{\begin{cases}\widehat{AEB}chung\\\widehat{EBD}=\widehat{EAB}\left(cmt\right)\end{cases}\Rightarrow\Delta EDB~\Delta EBA\left(g-g\right)}\)
\(\Rightarrow\frac{BE}{DE}=\frac{AE}{BE}\)
\(\Rightarrow BE^2=AE.DE\left(1\right)\)
Vì \(AC//MB\Rightarrow\widehat{ACM}=\widehat{DME}\left(SLT\right)\)
Ta có: \(\hept{\begin{cases}\widehat{ACM}=\widehat{ABD}\left(=\frac{1}{2}sđo\widebat{AD}\right)\\\widehat{ABD}=\widehat{MAD}\left(=\frac{1}{2}sđo\widebat{AD}\right)\end{cases}\Rightarrow\widehat{ACM}=\widehat{MAD}}\)
\(\Rightarrow\widehat{DME}=\widehat{MAD}\)
Xét tam giác EMD và tam giác EAM có:
\(\hept{\begin{cases}\widehat{DME}=\widehat{MAD}\\\widehat{AME}chung\end{cases}}\Rightarrow\Delta EMD~\Delta EAM\left(g-g\right)\)
\(\Rightarrow\frac{ME}{DE}=\frac{AE}{ME}\)
\(\Rightarrow ME^2=DE.AE\left(2\right)\)
Từ (1) và (2) \(\Rightarrow BE=ME\left(đpcm\right)\)
c) mai nốt :V
c) El à trung điểm MB;H là trung điểm AB
-> EH là đường trung bình tam giác MAB
=> EH// MA
=> góc EHB= góc MAB ( đồng vị )
Mà góc MAB = góc AKB ( = 1/2 số đo cung AB )
=> góc EHB= góc AKB
mà góc EHB+ góc IHB = 180 độ
=> góc AKB + góc IHB = 180 độ
=> BHIK nội tiếp
=> góc BHK= BIK mà góc BHK= 90 độ
=> góc BIK= 90 độ
=> AK vuông góc với BI

Mình giải câu 2
Góc AQB nội tiếp chắn cung AB
BAM góc tạo bởi dây cung chắn chung AB
Nên AQB = BAM
BAM=BKM góc nội tiếp chắn cung BM (do AKBM nội tiếp cái này phải chứng minh thêm MAOKM cùng thuộc đường tròn dễ)
suy ra AQB = BKM mà vị trí đồng vị nên suy ra các kiểu

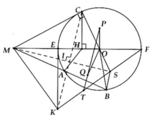
a, HS tự chứng minh
b, MH.MO = MA.MB ( = M C 2 )
=> ∆MAH:∆MOB (c.g.c)
=> M H A ^ = M B O ^
M B O ^ + A H O ^ = M H A ^ + A H O ^ = 180 0
=> AHOB nội tiếp
c, M K 2 = ME.MF = M C 2 Þ MK = MC
∆MKS = ∆MCS (ch-cgv) => SK = SC
=> MS là đường trung trực của KC
=> MS ^ KC tại trung của CK
d, Gọi MS ∩ KC = I
MI.MS = ME.MF = M C 2 => EISF nội tiếp đường tròn tâm P Þ PI = PS. (1)
MI.MS = MA.MB (= M C 2 ) => AISB nội tiếp đường tròn tâm Q Þ QI = QS. (2)
Mà IT = TS = TK (do DIKS vuông tại I). (3)
Từ (1), (2) và (3) => P, T, Q thuộc đường trung trực của IS => P, T, Q thẳng hàng
góc AHM=AIM=90
-> AHIM nội tiếp
b, dùng phương tích
nhưng hai góc đó không đối nhau