Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

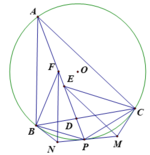
1). Gọi AD cắt (O) tại P khác A
Ta có P C M ^ = P A C ^ (góc tạo bởi tiếp tuyến và dây cung) = P E M ^ (góc đồng vị do E M ∥ A C );
Suy ra tứ giác ECMP nội tiếp. Từ đó suy ra M P C ^ = M E C ^ = E C A ^ = C A P ^ ⇒ PM tiếp xúc (O)
Tương tự PN tiếp xúc (O), suy ra MN tiếp xúc (O) tại P.


2) Theo 1). dễ thấy Δ B F A ∽ Δ B N P ⇒ Δ B N F ∽ Δ B P A ⇒ B N B P = F N A P (1).
Tương tự Δ C M E ∽ Δ C P A ⇒ C M C P = E M A P (2).
Từ (1) và (2), ta có B N C M ⋅ C P B P = F N E M và theo giả thiết F N E M = B N C M , suy ra C P = B P ⇒ A D là phân giác góc B A C ^ .

Tớ không vẽ hình được bạn tự vẽ nhé
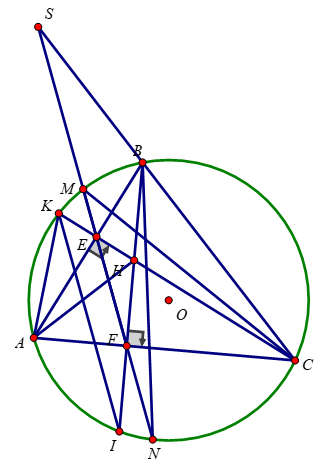
a, Vì K thuộc đường tròn đường kính AB
=> AKB=90
Mà CHA=90
=> tứ giác AKNH nội tiếp
Vậy tứ giác AKNH nội tiếp
b,Vì 2 tiếp tuyến cắt nhau tại M
nên \(OM\perp AC\)
=>\(OM//CB\)
=> tam giác AMO đồng dạng tam giác HCB
=> ĐPCM
c, Tứ giác AMKI nội tiếp do AIM=AKM=90
KIC=AMK
MÀ AMK=KNC do AM song song CH
=> KIC=KNC
=> tứ giác KINC nội tiếp
=>KNI=KCI
Mà KCI=KBA
=> KNI=KBA
=> IN song song AB
Vậy IN song song AB
Mình không viết kí hiệu góc nên bạn thông cảm

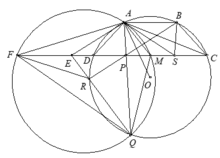
1). Gọi S điểm đối xứng với P qua M.Theo tính chất đối xứng của hình thang cân dễ thấy tứ giác ABSP cũng là hình thang cân.
Ta lại có Q P S ^ = Q A B ^ = Q R B ^ .
Từ đó có E P Q ^ = E R P ^ ⇒ Δ E R P ∽ Δ E P Q (g – g),
nên E Q P ^ = E P R ^ = B P S ^ = A S E ^ , suy ra tứ giác AEQS nội tiếp.
Do đó P A . P Q = P E . P S = P F 2 .2 P M = P F . P M , suy ra tứ giác A M Q F nội tiếp.
Từ đó suy ra đường tròn ngoại tiếp tam giác △ A Q F luôn đi qua M.

\(\text{a) Xét tứ giác BEFC có:}\)
\(\text{∠BEC = 90 o (CE là đường cao)}\)
\(\text{∠BFC = 90 ^0 (BF là đường cao)}\)
=> 2 đỉnh E, F cùng nhìn cạnh BC dưới 1 góc vuông
=> Tứ giác BEFC là tứ giác nội tiếp
\(\text{Xét tứ giác AEHF có:}\)
\(\text{∠AEH = 90 o (CE là đường cao)}\)
\(\text{∠AFH = 90 o (BF là đường cao)}\)
=> ∠AEH + ∠AFH = 180^ o
=> Tứ giác AEHF là tứ giác nội tiếp.
\(\text{b) Xét ΔSBE và ΔSFC có:}\)
\(\text{∠FSC là góc chung}\)
\(\text{∠SEB = ∠SCF (Tứ giác BEFC là tứ giác nội tiếp)}\)
=> ΔSBE ∼ ΔSFC (g.g)
\(\Rightarrow\frac{SB}{SF}\)=\(\frac{SE}{SC}\)\(\Rightarrow\text{SE.SF = SB.SC (1)}\)
\(\text{Xét ΔSMC và ΔSNB có:}\)
\(\text{∠ NSC là góc chung}\)
\(\text{∠ SCM = ∠SNB (Hai góc nội tiếp cùng chắn cung MB)}\)
=> ΔSMC ∼ ΔSBN (g.g)
\(\Rightarrow\frac{SM}{SB}\)=\(\frac{SC}{SN}\Rightarrow\text{SM.SN = SB.SC (2)}\)
Từ (1) và (2) => SE.SF = SM.SN
\(\text{c) Ta có:}\)
\(\hept{\begin{cases}\widehat{KAE}=\widehat{KCB}\left(\text{2 GÓC NỘI TIẾP CÙNG CHẮN CUNG KB}\right)\\\widehat{HAE}=\widehat{BFM}\left(\text{TỨ GIÁC AEHF LÀ TỨ GIÁC NỘI TIẾP}\right)\\\widehat{KCB}=\widehat{BFM}\left(\text{TỨ GIÁC BEFC LÀ TỨ GIÁC NỘI TIẾP}\right)\end{cases}}\)
=> ∠KAE = ∠HAE
=> AE là tia phân giác của góc ∠KAH
\(\text{Mà AE cũng là đường cao của tam giác KAH}\)
=> ΔKAH cân tại A
=> AE là đường trung tuyến của ΔKAH
=> E là trung điểm của KH hay K và H đối xứng nhau qua AB
\(\text{d) Tia BF cắt đường tròn (O) tại J}\)
∠KJB = ∠KCB (2 góc nội tiếp cùng chắn cung KB)
∠KCB = ∠EFH (tứ giác BEFC là tứ giác nội tiếp )
=> ∠KJB = ∠EFH
Mà 2 góc này ở vị trí so le trong
=> KJ // EF
KI // EF (gt)
=> I ≡ J
=> H, F, J thẳng hàng
HÌNH THÌ VÀO XEM THỐNG KÊ HỎI ĐÁP NHA
BÀI LÀM ĐÚNG MÀ SAO CÓ NGƯỜI K SAI TÔI ĐẢM BẢO BÀI NÀY ĐÚNG 100%

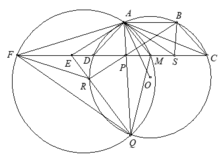
2). Vì EA là tiếp xúc (O) và từ kết quả câu 1) ta có E A 2 = E R . E Q = E P 2 .
Từ đó có E A = E P ⇒ D A P ^ = E A P ^ − E A D ^ = A P E ^ − A C D ^ = P A C ^
Do đó AP là phân giác D A C ^ ⇒ Q C = Q D ⇒ Q M ⊥ C D

1). Tam giác ABF và tam giác ACE ần lượt cân tại F, E và
F B A ^ = E C A ^ = A ^ 2 ⇒ Δ A B F ∽ Δ A C E .
2). Giả sử G là giao điểm của BE và CF.
Ta có G F G C = B F C E = A B A C = D B D C ⇒ G D ∥ F B , và F B ∥ A D ta có G ∈ A D .
3). Chứng minh B Q G ^ = Q G A ^ = G A E ^ = G A C ^ + C A E ^ = G A B ^ + B A F ^ = G A F ^ , nên AGQF nội tiếp, và Q P G ^ = G C E ^ = G F Q ^ , suy ra tứ giác FQGP nội tiếp.

Đặt bán kính của (I) và (O) lần lượt là \(r\) và \(R\).Gọi AI cắt (O) tại K khác A, KO cắt PQ, (O) lần lượt tại J,L.
Dễ thấy K là điểm chính giữa cung PQ và BC, suy ra KP = KQ, cũng dễ có KM = KN (1)
Áp dụng ĐL Cosin vào \(\Delta\)AKN ta có:
\(KN^2=AK^2+AN^2-2AK.AN.\cos45^0\Rightarrow KN^2=2R^2+2Rr+r^2\) (2)
Ta thấy OJ có độ dài bằng một nửa đường cao AH của \(\Delta\)ABC. Từ ĐL Ptolemy và Thales ta tính được:
\(AH=r.\frac{AB+AC+2R}{2R}=\frac{2Rr+r^2}{R}\Rightarrow OJ=\frac{2Rr+r^2}{2R}\)
Áp dụng hệ thức lượng tam giác vuông có:
\(KQ^2=KJ.KL=\left(R+\frac{2Rr+r^2}{2R}\right).2R=2R^2+2Rr+r^2\) (3)
Từ (1),(2) và (3) suy ra KM = KN = KP = KQ. Điều đó có nghĩa là M,N,P,Q cùng thuộc đường tròn tâm K (đpcm).