Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha
a) CM: tam giác ABE = tam giác HBE
Xét tam giác ABE (Â=90o) và tam giác HBE (góc H= 90o), ta có:
Góc ABE = Góc HBE ( BE là p/g góc B)
BE là cạnh chung
Vậy: tam giác ABE = tam giác HBE ( cạnh huyền-góc nhọn)
c) CM: NM=NC
Xét tam giác AEM và tam giác HEC, ta có:
góc AEM = góc HEC ( đối đỉnh)
AE = HE (tam giác ABE = tam gác HBE)
góc EAM = góc EHC = 90o
Vậy: tam giác AEM = tam giác HEC (g-c-g)
Ta có: AB+AM=BM
BH+HC=BC
mà BA=BH(tam giác BAE= tam giác BEH)
AM=HC(tam giác AEM= tam giác HEC)
nên BM=BC
Xét tam giác NBM và tam giác NBC, ta có:
NB là cạnh chung
góc NBM= góc NBC ( BE là p/g góc B)
BM=BC (cmt)
Vậy tam giác NBM= tam giác NBC ( c-g-c)
=> NM=NC ( 2 cạnh tương ứng)
Sorry vì mình khong làm được bài b

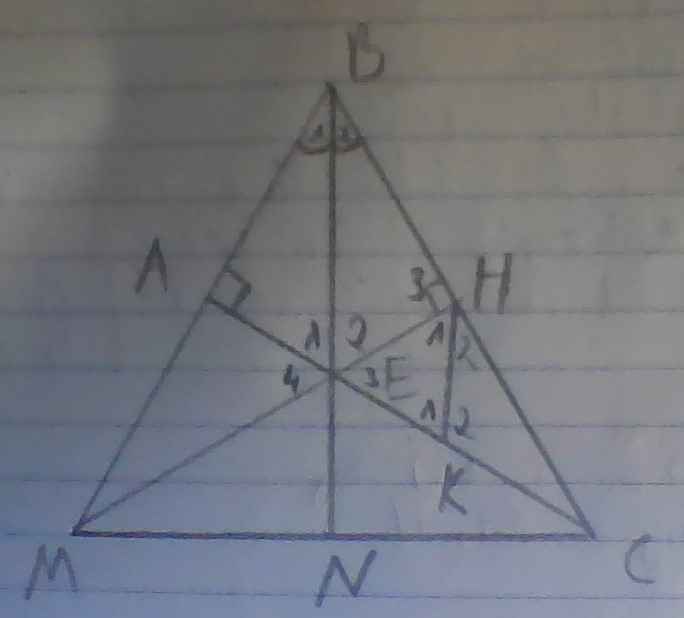
a) có BE là tia p/g của góc ABC
=> góc B1 = góc B2 = góc ABC/2 = 600 /2 = 300
có △ABC vuông tại A => △ABE vuông tại A
EH⊥BC=> △HBE vuông tại H
Xét △ vuông ABE và △vuông HBE có
góc B1 = góc B2
BE chung
=>△ vuông ABE =△vuông HBE ( cạnh huyền - góc nhọn)
b) có △ABE vuông tại A=> góc B1 + góc E1 = 900
góc E1 = 600 ( vì góc B1 = 300)
có △ vuông ABE =△vuông HBE
=> góc E1 = góc E2
mà HK//BE => góc E1 = góc K1 (ĐV)
và góc E2 = góc H1 (SLT)
=> góc E1 = góc E2 = góc K1=góc H1 = 600
=> △HEK đều
c) có góc E1 = góc E2 ; góc E3 = góc E4
=>góc E1 +góc E4 = góc E2 + góc E3
=> góc BEM= góc BEC
Xét △BEM và △ BEC có
góc B1 = góc B2
BE chung
góc BEM= góc BEC
=> △BEM = △ BEC (g.c.g)
=>BM=BC
=>△BMC cân tại B
trong △BMC có BN là đường p/g xuất phát từ đỉnh B
lại có △BMC cân tại B
=> BN cũng là đường trung tuyến xuất phát từ đỉnh B
=> N là trung điểm của MC
=> NM=NC

Bạn tự vẽ hình nha.
a,Xét tg ABE và tg HBE:
^BAE=^BHE=90*
^ABE=^HBE(BE là pg)
BE chung
=>tg ABE= tg HBE(ch-gn)
b,+,tg ABC có:^BAC=90*,^ABC=60*
=>^C=30*
+,tg BHE có: ^BHE=90*,^EBH=30*(^EHB=1/2ABC)
=>^HEB=60*
Mà HK // BE
=>^HBE=^EHK=60*(slt)
+, tg CHE có:^EHC=90*,^C=30*
=>HEC=60*
+,tg HEK có:
^EHK=60*,^HEC(^HEK)=60*
=>TG HEK đều(dhnb)
Phần c mik chỉ ghi các bước thôi còn bạn tự chình bày nhé.
c, +,CM:tg AEM=tg HEC(cgv-gnk)
=>AM=HC
+,CM:BM=BC
+,CM:tg BMI=tgBCI(cgc)
=>NM=NC
Xong r nha. Chúc bạn học tốt.

Bài 5:
a) Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))
Do đó: ΔABE=ΔHBE(cạnh huyền-góc nhọn)

a.Xét △ABE vuông tại A và △HBE vuông tại H có :
BE chung
góc ABE = góc HBE (vì BE là tia phân giác)
=>△ABE = △HBE (cạnh huyền - góc nhọn)
b. Vì △ABE = △HBE (chứng minh trên)
=>AB = HB (2 cạnh tương ứng)
=> △AHB cân tại B
mà BE là tia phân giác của góc ABC (giả thuyết)
nên BE đồng thời là đường trung trực của đoạn thẳng AH.

a: Xét ΔBAH vuông tại A và ΔBEH vuông tại E có
BH chung
góc ABH=góc EBH
=>ΔBAH=ΔBEH
=>BA=BE
=>ΔBAE cân tại B
b: Xét ΔBFC có
FE,CA là đường cao
FE cắt CA tại H
=>H là trực tâm
=>HK vuông góc FC
c: Xét tứ giác QAKF có
M là trung điểm chung của QK và AF
=>QAKF là hình bình hành
=>QA//FK
=>Q,E,A thẳng hàng
Bạn tự vẽ hình nha
Xét hai \(\Delta\) vuông ABE và HBE có:
BE là cạnh huyền chung
\(\widehat{ABE}=\widehat{HBE}\left(gt\right)\)
Vậy \(\Delta ABE=\Delta HBE\left(ch-gn\right)\)
b) ΔABC vuông tại A
\(\Rightarrow\widehat{ABC}+\widehat{ACB}=90^o\)
Mà \(\widehat{ABC}=60^o\)
\(\Rightarrow\widehat{ACB}=30^o\)
ΔEHC vuông tại H
\(\Rightarrow\widehat{HEC}+\widehat{HCE}=90^o\)
Mà \(\widehat{HCE}=30^o\)
\(\Rightarrow\widehat{HEC}=60^o\left(1\right)\)
Ta lại có : \(\widehat{ABE}=\widehat{EBH}=\frac{\widehat{ABC}}{2}=\frac{60^o}{2}=30^o\)
ΔBEH vuông tại H
\(\widehat{EBH}+\widehat{BEH}=90^o\)
Mà \(\widehat{EBH}=30^o\)
\(\Rightarrow\widehat{BEH}=60^o\)
Vì HK // BE
\(\Rightarrow\widehat{BEH}=\widehat{EHK}\) (2 góc so le trong bằng nhau)
Mà \(\widehat{BEH}=60^o\)
nên \(\widehat{EHK}=60^o\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\)ΔEHK là tam giác đều
c) Xét hai tam giác vuông AEM và HEC có:
AE = HE (ΔABE=ΔHBE)
\(\widehat{AEM}=\widehat{HEC}\) (2 góc đối đỉnh)
Vậy: ΔAEM=ΔHEC(cgv−gn)
\(\Rightarrow\)AM = HC (hai cạnh tương ứng)
Ta có: BM = BA + AM
BC = BH + HC
Mà BA = BH (ΔABE=ΔHBE)
AM = HC (cmt)
⇒ BM = BC
⇒ΔBMC cân tại B
⇒ BN là đường phân giác đồng thời là đường trung tuyến của \(\Delta\) BMC
Nên NM = NC
tự vẽ hình bn nha
a) vì BE là p/g của góc B =>góc B1=góc B2
xét tam giác ABE vg tại A và tam giác HBE vg tại H có :
BE chung
góc B1=góc B2( cmt)
=> tam giác ABE = tam giác HBE ( ch-gn)
nhớ tick cho mk