Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a) Ta có:
\(S=1-3+3^2-3^3+3^4-3^5+3^6-3^7+...+3^{96}-3^{97}+3^{98}-3^{99}\)
\(=\left(1-3+3^2-3^3\right)+\left(3^4-3^5+3^6-3^7\right)+...+\left(3^{96}-3^{97}+3^{98}-3^{99}\right)\)
\(=1.\left(1-3+3^2-3^3\right)+3^4.\left(1-3+3^2-3^3\right)+...+3^{96}.\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(-20\right)\) \(\text{⋮}\) \(-20\)
Vậy \(S\) \(\text{⋮}\) \(-20\)
Bài 1:
Ta có:
\(A=\left(5m^2-8m^2-9m^2\right).\left(-n^3+4n^3\right)\)
\(=\left[\left(5-8-9\right).m^2\right].\left[\left(-1+4\right).n^3\right]\)
\(=\left(-12\right).m^2.3.n^3\)
\(=\left(m^2.3\right).\left[\left(-12\right)n^3\right]\)
Xét: \(m^2\ge0\) với V m
3>0 nên \(m^2.3\ge0\) với V m
Như vậy để \(A\ge0\) thì \(\left(-12\right)n^3\ge0\)
-12 < 0 nên nếu \(\left(-12\right)n^3\ge0\) thì \(n^3<0\Rightarrow n<0\)
Vậy với n<0 và mọi m thì \(A\ge0\)

Có u 10 = 2 9 u
log u 1 + 2 + log u 1 - 2 log u 10 = 2 log u 10 .
Đặt t = 2 log u 10 - log u 1
PT 2 - t = t ⇔ t = 1
Có
2 log u 10 - log u 1 = 18 log 2 + l og u 1 = 1 ⇔ u 1 = 10 1 - 18 log 2
Có u n = u 1 . 2 n - 1 = 10 1 - 18 log 2 . 2 n - 1
Giải u n > 5 100 ⇔ n = 248
Đáp án cần chọn là B

Đáp án B
Đặt t = log u 1 , khi đó giả thiết ⇔ t 3 - 2 t 2 + t - 2 = 0 ⇔ t - 2 t 2 + 1 = 0 ⇔ t = 2 ⇒ log u 1 = 2
Ta có u n + 1 = 2 u n + 10 ⇔ u n + 1 + 10 = 2 u n + 10 ⇔ v n + 1 = 2 v n với v n = u n + 10
Dễ thấy v n + 1 = 2 v n là một cấp số nhân với công bội q = 2 ⇒ v n = v 1 . 2 n - 1
Mà log u 1 = 2 ⇒ u 1 = 10 2 = 100 suy ra v 1 = u 1 + 10 = 110 ⇒ v n = 100 . 2 n - 1
Khi đó u n = v n - 10 = 100 . 2 n - 1 - 10 > 10 100 - 10 ⇔ 2 n - 1 > 10 98 ⇔ n > log 2 10 98 + 1 = 326 , 54
Vậy giá trị nhỏ nhất của n cần tìm là n m i n = 327 .
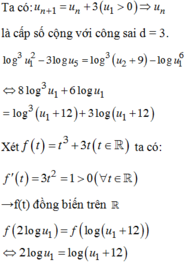
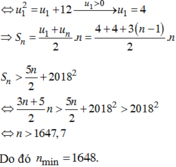
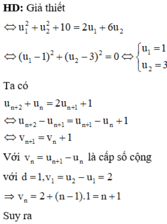
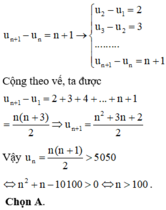

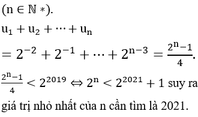
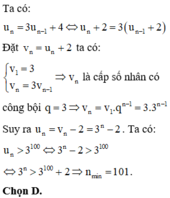


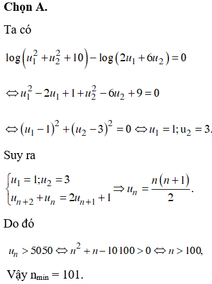
Chọn đáp án D
Vậy số tự nhiên n nhỏ nhất thỏa mãn điều kiện trên là n 0 = 201