Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBDC có
M là trung điểm của BC
ME//BD
Do đó: E là trung điểm của CD
=>AD=DE=CE
b: Xét ΔAME có
D là trung điểm của AE
DI//ME
Do đó: I là trung điểm của AM
Xét ΔBAM có BI là đường trung tuyến
nen \(S_{ABI}=S_{MBI}\)

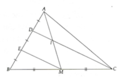
a) Ta có EM là đường trung bình của tam giác BCD Þ ĐPCM.
b) DC đi qua trung điểm D của AE và song song với EM Þ DC đi qua trung điểm I của AM.
c) Vì DI là đường trung bình của tam giác AEM nên DI = (1/2) EM.(1)
Tương tự, ta được: EM = (1/2)DC (2)
Từ (1) và (2) Þ DC = 4DI

1

a
Xét tam giác BDC có M là trung điểm của BC,ME//BD nên E là trung điểm của DC hay DE=CE.
Xét tam giác AME có I là trung điểm của AM,ID//ME nên D là trung điểm của AE hay AD=DE.
Suy ra AD=DE=CE.
b
Ta có ID là đường trung bình nên \(ID=\frac{1}{2}ME\)
ME là đường trung bình nên \(ME=\frac{1}{2}BD\Rightarrow DI=\frac{1}{4}BD\)
2

a
Kẻ ME//AC cắt BD tại E.
Ta có:ME//AC,M là trung điểm của BC nên E là trung điểm của BD.
Khi đó ME là đường trung bình nên \(ME=\frac{1}{2}DC=AD\)
Xét \(\Delta\)ADI và \(\Delta\)MIE có:ME=AD;\(\widehat{IAD}=\widehat{IME}\);\(\widehat{IDA}=\widehat{IEM}\)
\(\Rightarrow\Delta ADI=\Delta MIE\left(g.c.g\right)\Rightarrow ID=IE\)
b
Kẻ MF//BD cắt AC tại F
Ta có:
M là trung điểm của BC,MF//BD nên F là trung điểm của DC.Khi đó D là trung điểm của AF,I là trung điểm của AM nên:
\(DI=\frac{1}{2}MF\)
Mặt khác:EM//DC;ED//MF nên theo tính chất cặp đoạn chắn ta được MF=ED.
\(\Rightarrow DI=\frac{1}{2}BE\Rightarrow ID=\frac{1}{2}IB\)
a: Xét ΔBDC có
M là trung điểm của BC
ME//BD
Do đó: E là trung điểm của DC
Suy ra: \(ED=EC=\dfrac{DC}{2}\)
mà \(AD=\dfrac{DC}{2}\)
nên AD=ED=EC