Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(P\left(1\right)=1-a+b-c+d-2010=-2011\)
\(\Rightarrow a-b+c-d=2\)
\(P\left(-1\right)=-1-a-b-c-d-2010=-2045\)
\(\Rightarrow a+b+c+d=34\)
\(\Rightarrow\hept{\begin{cases}2b+2d=32\\2a+2c=36\end{cases}}\Leftrightarrow\hept{\begin{cases}b+d=16\\a+c=18\end{cases}}\)
\(P\left(2\right)=32-16a+8b-4c+2d-2010\)
\(=-12a-4\left(a+c\right)+2\left(b+d\right)+6b-1978\)
\(=-12a-4.18+2.16+6b-1978\)
\(=-12a+6b-2018=-2084\)
\(\Rightarrow2a-b=11\)
\(P\left(3\right)=243-81a+27b-9c+3d-2010\)
\(=243-72a-9\left(a+c\right)+3\left(b+d\right)+24b-2010\)
\(=243-72a+24b-9.18+3.16-2010=-2385\)
\(\Rightarrow-72a+24b=-504\Rightarrow3a-b=21\)
Từ đó ta có \(\hept{\begin{cases}2a-b=11\\3a-b=21\end{cases}\Rightarrow\hept{\begin{cases}a=10\\b=9\end{cases}\Rightarrow}\hept{\begin{cases}c=8\\d=7\end{cases}}}\)
Vậy đa thức cần tìm là \(f\left(x\right)=x^5+10x^4+9x^3+8x^2+7x-2010\)

+ P(x) chia hết cho x + 1
⇔ P(-1) = 0
⇔ m . ( - 1 ) 3 + ( m – 2 ) ( - 1 ) 2 – ( 3 n – 5 ) . ( - 1 ) – 4 n = 0
⇔ -m + m – 2 + 3n – 5 – 4n = 0
⇔ -n – 7 = 0
⇔ n = -7 (1)
+ P(x) chia hết cho x – 3
⇔ P(3) = 0
⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0
⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0
⇔ 36m – 13n = 3 (2)
Từ (1) và (2) ta có hệ phương trình :
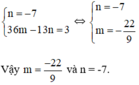

+ P(x) chia hết cho x + 1
⇔ P(-1) = 0
⇔ m.(-1)3 + (m – 2)(-1)2 – (3n – 5).(-1) – 4n = 0
⇔ -m + m – 2 + 3n – 5 – 4n = 0
⇔ -n – 7 = 0
⇔ n = -7 (1)
+ P(x) chia hết cho x – 3
⇔ P(3) = 0
⇔ m.33 + (m – 2).32 – (3n – 5).3 – 4n = 0
⇔ 27m + 9m – 18 – 9n + 15 – 4n = 0
⇔ 36m – 13n = 3 (2)
Từ (1) và (2) ta có hệ phương trình :
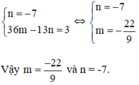

a) Ta có f(x) - 5 \(⋮\)x + 1
=> x3 + mx2 + nx + 2 - 5 \(⋮\)x + 1
=> x3 + mx2 + nx - 3 \(⋮\)x + 1
=> x = - 1 là nghiệm đa thức
Khi đó (-1)3 + m(-1)2 + n(-1) - 3 = 0
<=> m - n = 4 (1)
Tương tự ta được f(x) - 8 \(⋮\)x + 2
=> x3 + mx2 + nx - 6 \(⋮\) x + 2
=> x = -2 là nghiệm đa thức
=> (-2)3 + m(-2)2 + n(-2) - 6 = 0
<=> 2m - n = 7 (2)
Từ (1)(2) => HPT \(\left\{{}\begin{matrix}m-n=4\\2m-n=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\n=-1\end{matrix}\right.\)
Vậy đa thức đó là f(x) = x3 + 3x2 - x + 2
b) f(x) - 7 \(⋮\)x + 1
=> x3 + mx + n - 7 \(⋮\) x + 1
=> x = -1 là nghiệm đa thức
=> (-1)3 + m(-1) + n - 7 = 0
<=> -m + n = 8 (1)
Tương tự ta được : x3 + mx + n + 5 \(⋮\)x - 3
=> x = 3 là nghiệm đa thức
=> 33 + 3m + n + 5 = 0
<=> 3m + n = -32 (2)
Từ (1)(2) => HPT : \(\left\{{}\begin{matrix}3m+n=-32\\-m+n=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4m=-40\\-m+n=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=-10\\n=-2\end{matrix}\right.\)
Vậy f(x) = x3 - 10x -2
Áp dụng định lý Bê-du, ta có :
Khi \(P\left(x\right)\)chia hết cho \(x-2\Rightarrow P\left(2\right)=0\)
\(\Rightarrow6.2^5+a.2^4+b.2^3+2^2+c.2+450=0\)
\(\Rightarrow192+16a+8b+4+2c+450=0\)
\(\Rightarrow16a+8b+2c=-646\)
\(\Rightarrow8a+4b+c=-323\)
Khi \(P\left(x\right)\)chia hết cho \(x-3\Rightarrow P\left(3\right)=0\)
\(\Rightarrow P\left(3\right)=6.3^5+a.3^4+b.3^3+3^2+3c+450=0\)
\(\Rightarrow1458+81a+27b+9+3c+450=0\)
\(\Rightarrow81a+27b+3c=-1917\)
\(\Rightarrow27a+9b+c=-639\)
Khi \(P\left(x\right)\)chia hết cho \(x-5\Rightarrow P\left(5\right)=0\)
Làm tương tự, có :
\(125a+25b+c=-3845\)
Bạn tự xét phần tiếp theo vì ở đây đã có 3 dữ kiện để tìm a, b , c rồi.