Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thay x = -1; x = 5 vào đa thức f(x) = x2 – 4x – 5, ta có:
f(-1) = (-1)2 – 4.(-1) – 5 = 1 + 4 – 5 = 0
f(5) = 52 – 4.5 – 5 = 25 – 20 – 5 = 0
Vậy x = -1 và x = 5 là các nghiệm của đa thức f(x) = x2 – 4x – 5

Thay x = -1; x = 5 vào đa thức f(x) = x2 – 4x – 5, ta có:
f(-1) = (-1)2 – 4.(-1) – 5 = 1 + 4 – 5 = 0
f(5) = 52 – 4.5 – 5 = 25 – 20 – 5 = 0
Vậy x = -1 và x = 5 là các nghiệm của đa thức f(x) = x2 – 4x – 5
Thay x = -1; x = 5 vào đa thức f(x) = x2 – 4x – 5, ta có:
f(-1) = (-1)2 – 4.(-1) – 5 = 1 + 4 – 5 = 0
f(5) = 52 – 4.5 – 5 = 25 – 20 – 5 = 0
Vậy x = -1 và x = 5 là các nghiệm của đa thức f(x) = x2 – 4x – 5

f(-1)=(-1)2-4(-1)-5
=1+4-5
=0
f(5)=52-4x5-5
=25-20-5
=0
vậy x=-1 và x=5 là nghiệm của đa thức

Với x = -1
Ta có: f(-1) = (-1)2 - 4.(-1) - 5 = 0
Với x = 5
Ta có: f(x) = 52 - 4.5 -5 = 0
Vậy x = -1, x = 5 là nghiệm của đa thức f(x)
Thay x = -1 vào đa thức f(x) ta đc:
f(1) = (-1)2 - 4.(-1) - 5 = 1 + 4 -5 = 0
Vậy x = -1 là nghiệm của đa thức f(x) = x2 - 4x - 5
Thay x = 5 vào đa thức f(x) ta đc:
f(5) = 52 - 4.5 - 5 = 25 - 20 - 5 = 0
Vậy x = 5 là nghiệm của đa thức f(x) = x2 - 4x - 5

` P(x) = x^3-2x^2+x-2`
`Q(x) = 2x^3 - 4x^2+ 3x – 56`
a) `P(x) -Q(x)`
`= x^3-2x^2+x-2 - 2x^3 +4x^2 -3x +56`
`=(x^3-2x^3) +(4x^2-2x^2) +(x-3x) +(-2+56)`
`= -x^2 +2x^2 -2x +54`
b) Thay `x=2` vào `P(x)` ta đc
`P(2) = 2^3 -2*2^2 +2-2`
`= 8-8+2-2 =0`
Vậy chứng tỏ `x=2` là nghiệm của đa thức `P(x)`
Thay `x=2` vào `Q(x)` ta đc
`Q(2) = 2*2^3 -4*2^2 +3*2-56`
`=16 -16+6-56`
`= -50`
Vậy chứng tỏ `x=2` là ko nghiệm của đa thức `Q(x)`

TA CÓ
\(p\left(\frac{1}{2}\right)=4\cdot\left(\frac{1}{2}\right)^2-4\cdot\frac{1}{2}+1=4\cdot\frac{1}{4}-2+1\)
\(=1-2+1=0\)
vậy ......
TA CÓ
\(x^2\ge0\Rightarrow4x^2\ge0\Rightarrow4x^2+1\ge1\)hay\(4x^2+1>0\)
vậy..............
Thay \(x=\frac{1}{2}\)vào P (x) ta có:
\(P\left(\frac{1}{2}\right)=4.\left(\frac{1}{2}\right)^2-4.\frac{1}{2}+1\)
\(P\left(\frac{1}{2}\right)=4.\frac{1}{4}-2+1\)
\(P\left(\frac{1}{2}\right)=1-2+1\)
\(P\left(\frac{1}{2}\right)=0\)
Vậy \(x=\frac{1}{2}\) là nghiệm của P(x)

1) \(\left(x^2-4x+3\right)f\left(x+1\right)=\left(x-2\right)f\left(x-1\right)\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)f\left(x+1\right)=\left(x-2\right)f\left(x-1\right)\)
Với \(x=1\): \(0=-1f\left(0\right)\Leftrightarrow f\left(0\right)=0\)do đó \(0\)là một nghiệm của đa thức \(f\left(x\right)\).
Tương tự xét \(x=2,x=3\)có thêm hai nghiệm nữa là \(3\)và \(2\).
2) \(f\left(2\right)=4a-2+b=0\Leftrightarrow4a+b=2\)
Tổng hệ số cao nhất và hệ số tự do là \(a+b\)suy ra \(a+b=-7\).
Ta có hệ:
\(\hept{\begin{cases}4a+b=2\\a+b=-7\end{cases}}\Leftrightarrow\hept{\begin{cases}3a=9\\b=-7-a\end{cases}}\Leftrightarrow\hept{\begin{cases}a=3\\b=-10\end{cases}}\).
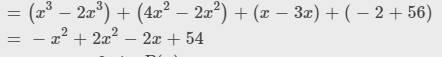
f(-1)=1+4-5=0
f(5)=25-20-5=0
Do đó: x=-1; x=5 là các nghiệm của f(x)
Ta có \(f\left(-1\right)=1+4-5=0\)
Vậy x = -1 là nghiệm đa thức trên
\(f\left(5\right)=25-20-5=0\)
Vậy x = 5 là nghiệm đa thức trên