Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn 2 đỉnh liền kề của đa giác: có n cách chọn
Chọn 1 đỉnh còn lại ko kề với 2 đỉnh đã chọn :n-4 cách
\(\Rightarrow n\left(n-4\right)\) tam giác có đúng 1 cạnh là cạnh của đa giác
\(n\left(n-4\right)=165\Rightarrow n=15\)

a. Đa giác n đỉnh có \(C_n^2\) đoạn thẳng nối các đỉnh
Trong đó có n cạnh (là đường nối 2 đỉnh liền kế)
\(\Rightarrow\) Có \(C_n^2-n\) đường chéo
b. Cứ 3 đỉnh tạo thành 1 tam giác nên số tam giác là: \(C_n^3\)
c. Tam giác có 2 cạnh là 2 cạnh của tam giác khi 3 đỉnh của tam giác là 3 đỉnh liền kề
\(\Rightarrow\) có n tam giác thỏa mãn
d. Số tam giác chỉ có 1 cạnh là cạnh đa giác: có n cách chọn 2 điểm liền kề, ta có \(n-4\) cách chọn 1 điểm còn lại ko kề với 2 điểm trên
\(\Rightarrow n\left(n-4\right)\) tam giac thỏa mãn
e. Số tam giác thỏa mãn: \(C_n^3-\left(n+n\left(n-4\right)\right)\)

Đáp án D
Ta đánh số các đỉnh của đa giác từ 1 đến 15, gọi 4 đỉnh của tứ giác là a, b, c, d (theo thứ tự).
Ta xét 2 trường hợp sau:
Trường hợp 1: a = 1. Vì không thể là cạnh kề đa giác nên không thể có 2 cạnh kề nhau. Nên
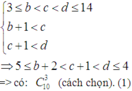
Trường hợp 2: a > 1. Tương tự:
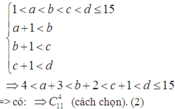
Từ (1) và (2) ta có tổng số tứ giác thỏa mãn: C 10 3 + C 11 4 = 450 .
Tổng quát: Đa giác có n đỉnh số tứ giác lập thành từ 4 đỉnh
Không có cạnh của đa giác là: n 4 . C n - 5 3 .

Chọn B
Lấy ba điểm phân biệt không thẳng hàng sẽ tạo thành một tam giác nên số tam giác tạo thành là:
![]()

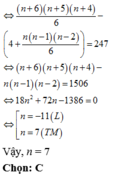
Chọn D
Lời giải. Số tam giác tạo thành có 3 đỉnh là 3 đỉnh của đa giác là C n 3
Số tam giác tạo thành có đúng 2 cạnh là cạnh của đa giác là n
Số tam giác tạo thành có đúng 1 cạnh là cạnh của đa giác là n(n-4)
(điều kiện n ∈ ℕ v à n < 4 )
→ số tam giác tạo thành không có cạnh nào là cạnh của đa giác là
Theo giả thiết, ta có
⇔ n = 35 ( t h ỏ a m ã n ) n = 4 ( l o ạ i )