
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



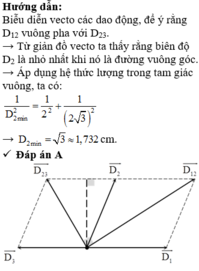
Đáp án A
Cách 1: Dùng giản đồ vectơ
Xây dựng giãn đồ vectơ như hình vẽ.
Ta thấy vectơ A2 đạt giá trị nhỏ nhất khi và chỉ khi vectơ A2 trùng với OH.
Áp dụng hệ thức lượng trong tam giác vuông
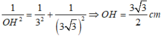
![]()
Cách 2
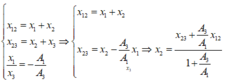
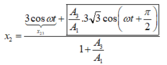
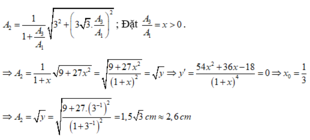


Trong toán học khi bài toán yêu cầu tìm cực trị thì các em đạo hàm của hàm y sau đó xét y’=0 và lập bảng biến thiên để xét giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN). Tuy nhiên thông thường đối với bài toán vật lý hàm y có nghĩa khi nghiệm đó là nghiệm dương, khi đó đề hỏi GTLN hoặc GTNN thì khi đạo hàm của hàm y thì chỉ có duy nhất 1 nghiệm dương (tức là tồn tại GTLN thì không tồn tại GTLN và ngược lại). Do đó chúng ta không cần vẽ bảng biến thiên mà kết luận ngay tại giá trị x0 nào đó (x0 là nghiệm dương duy nhất của hàm y’) hàm đạt GTLN (GTNN).

\(x=x_1+x_2\Rightarrow x_2=x-x_1=2-5=-3cm\)
Ta có: \(x_1=10\cos(5\pi t)=5\Rightarrow 5\pi t=\pi/3\)
Suy ra \(x_2=A_2\cos(\dfrac{\pi}{3}+\dfrac{\pi}{3})=-0,5A_2=-3\)
\(\Rightarrow A_2 = 6cm\)
Vậy biên độ tổng hợp: \(A^2=10^2+6^2+2.10.6\cos(\pi/3)=196\)
\(\Rightarrow A = 13cm\)

Biểu diễn hai vecto A1 và A2 độ lớn lần lượt là √3/2 cm, √3 cm hợp với trục Ox lần lượt các góc 90o và 150o.
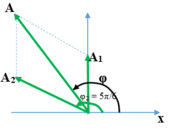
Ta có công thức :
A2 = A12 + A22 + 2A1A2 cos(φ2 - φ1) ⇒ A = 2,3 cm
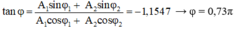
Vậy phương trình tổng hợp là: x = 2,3cos(5πt + 0,73π) (cm)

Đáp án A
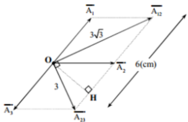
x12 = x1 + x2; x23 = x2 + x3
![]()
![]()
Do dao động D1 ngược pha với D3 nên dao động D1 cùng pha với –D3 có nghĩa là cùng pha với D1-3 =>
![]()
Từ giản đồ véc tơ ta có:
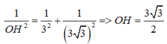
![]()