
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
P = s i n 2 90 ° − α + s i n 2 α = c o s 2 α + s i n 2 α = 1

Chọn C.
Nhân cả tử và mẫu với tanα và chú ý tanα.cotα = 1 ta được:

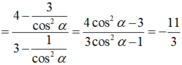

\(tana-cota=2\sqrt{3}\Rightarrow\left(tana-cota\right)^2=12\)
\(\Rightarrow\left(tana+cota\right)^2-4=12\Rightarrow\left(tana+cota\right)^2=16\)
\(\Rightarrow P=4\)
\(sinx+cosx=\dfrac{1}{5}\Rightarrow\left(sinx+cosx\right)^2=\dfrac{1}{25}\)
\(\Rightarrow1+2sinx.cosx=\dfrac{1}{25}\Rightarrow sinx.cosx=-\dfrac{12}{25}\)
\(P=\dfrac{sinx}{cosx}+\dfrac{cosx}{sinx}=\dfrac{sin^2x+cos^2x}{sinx.cosx}=\dfrac{1}{sinx.cosx}=\dfrac{1}{-\dfrac{12}{25}}=-\dfrac{25}{12}\)

Chọn D.
Ta có ![]() tương đương
tương đương ![]()
do đó; cos α = |cos α|
suy ra; cosα ≥ 0
Điểm cuối của góc lượng giác α ở góc phần tư thứ I hoặc IV.
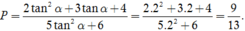

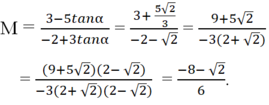
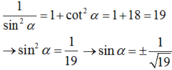
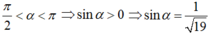
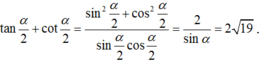
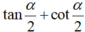 bằng:
bằng: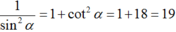
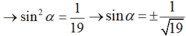
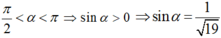

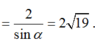
Lời giải:
\(A=\frac{\sin ^2a+1}{2\sin ^2a+3\cos ^2a}=\frac{2\sin ^2a+\cos ^2a}{2\sin ^2a+3\cos ^2a}=\frac{2+\cot ^2a}{2+3\cot ^2a}=\frac{2+2^2}{2+3.2^2}=\frac{3}{7}\)
Em vẫn chưa hiểu bước biến đổi từ 1 sang 2 ;-;