Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Theo tính chất đường phân giác ta có : \(\frac{AD}{AB}=\frac{DC}{BC}\)=> \(\frac{AD}{4}=\frac{DC}{6}\)=> \(\frac{AD}{2}=\frac{DC}{3}=\frac{AD+DC}{2+3}=\frac{AC}{5}=\frac{5}{5}=1\)
=> \(\hept{\begin{cases}AD=2\\DC=3\end{cases}}\)
a) Áp dụng tính chất đường phân giác ta có:
\(\frac{AD}{CD}=\frac{AB}{BC}=\frac{4}{6}=\frac{2}{3}\)
\(\Leftrightarrow\frac{AD}{2}=\frac{AB}{3}=\frac{AD+AB}{2+3}=1\)
\(\Leftrightarrow AD=2;AB=3\)

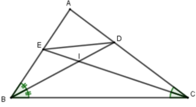
Ta có: A D A B = D C B C (t/c)
⇒ A D 4 = D C 6 = A D + D C 4 + 6 = 5 10 = 1 2
=> AD = 4. 1 2 = 2, DC = 6. 1 2 = 3
Suy ra:
D I I B = D C C B = 3 6 = 1 2 ⇒ D I D B = 1 3 B E E A = B C A C = 6 5 ⇒ B E B A = 6 11 A D D C = 2 3 ⇒ A D A C = 2 5
Suy ra S D I E = 1 3 S B D E
⇒ S D I E = 1 3 . 6 11 . 2 5 = 4 55 S A B C
Vậy S D I E S A B C = 4 55
Đáp án: A

a: Xét ΔABE vuông tại E và ΔACK vuông tại K có
góc BAE chung
Do đó; ΔABE\(\sim\)ΔACK
Suy ra: AE/AK=AB/AC=5/7
hay AK/AE=7/5
b: Xét ΔAEK và ΔABC có
AE/AB=AK/AC
góc EAK chung
Do đó: ΔAEK\(\sim\)ΔABC

a, Ta có : \(\frac{BE}{BC}=\frac{BF}{BA}\Rightarrow\frac{BE}{BF}=\frac{BC}{AB}=\frac{12}{9}\)
Vậy \(\frac{BE}{BC}=\frac{BF}{BA}=\frac{12}{9}=\frac{4}{3}\)
b, Xét tam giác BAF và tam giác BCE ta có :
^B _ chung
\(\frac{BE}{BC}=\frac{BF}{BA}=\frac{3}{4}\)( cmt )
Vậy tam giác BAF ~ tam giác BCE ( c.g.c )
Sửa hộ \(\frac{BA}{BC}=\frac{BF}{BE}=\frac{4}{3}\)
do \(\frac{BE}{BC}=\frac{BF}{BA}\Rightarrow\frac{BA}{BC}=\frac{BF}{BE}\)