Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P=\dfrac{6x+6y+2xy}{2}=\dfrac{6x+6y+2xy+10-10}{2}\)
\(=\dfrac{6x+6y+2xy+2\left(x^2+y^2\right)+6}{2}-5\)
\(=\dfrac{\left(x+y+2\right)^2+\left(x+1\right)^2+\left(y+1\right)^2}{2}-5\ge-5\)
\(P_{min}=-5\) khi \(x=y=-1\)

Ta có: T = x 3 + y 3 − x 2 + y 2 x − 1 y − 1 = x 2 x − 1 + y 2 y − 1 x − 1 y − 1 = x 2 y − 1 + y 2 x − 1
Do x > 1 , y > 1 nên x − 1 > 0 , y − 1 > 0
Áp dụng bất đẳng thức Cauchy cho 2 số dương x 2 y − 1 , y 2 x − 1 ta có:
x − 1 + 1 ≥ 2 x − 1 ⇔ x − 1 − 1 2 ≥ 0 ⇔ x − 2 x − 1 ≥ 0 ⇔ x x − 1 ≥ 2 y − 1 + 1 ≥ 2 y − 1 ⇔ y − 1 − 1 2 ≥ 0 ⇔ y − 2 y − 1 ≥ 0 ⇔ x y − 1 ≥ 2
Do đó: T = x 2 y − 1 + y 2 x − 1 ≥ 2 x y x − 1 . y − 1 ≥ 8
Dấu “=” xẩy ra khi x 2 y − 1 = y 2 x − 1 x − 1 = 1 y − 1 = 1 ⇔ x = 2 y = 2 (thỏa mãn điều kiện)
Vậy giá trị nhỏ nhất của biểu thứcT= 8 khi x=y= 2

Ta có:
P = 1 x ( 1 z 2 + 1 y 2 ) + 1 y ( 1 z 2 + 1 x 2 ) + 1 z ( 1 x 2 + 1 y 2 )
Đặt: 1 x = a ; 1 y = b ; 1 z = c thì a,b,c>0 và a2+b2+c2=1
P = a b 2 + c 2 + b c 2 + a 2 + c a 2 + b 2 = a 2 a ( 1 − a 2 ) + b 2 b ( 1 − b 2 ) + c 2 c ( 1 − c 2 )
Áp dụng bất đẳng thức Côsi cho 3 số dương ta có:
a 2 1 - a 2 2 = 1 2 .2 a 2 ( 1 − a 2 ) ( 1 − a 2 ) ≤ 1 2 2 a 2 + 1 − a 2 + 1 − a 2 3 = 4 27 = > a ( 1 − a 2 ) ≤ 2 3 3 < = > a 2 a ( 1 − a 2 ) ≥ 3 3 2 a 2 ( 1 )
Tương tự: b 2 b ( 1 − b 2 ) ≥ 3 3 2 b 2 ( 2 ) ; c 2 c ( 1 − c 2 ) ≥ 3 3 2 c 2 ( 3 )
Từ (1); (2); (3) ta có P ≥ 3 3 2 ( a 2 + b 2 + c 2 ) = 3 3 2
Đẳng thức xảy ra a = b = c = 1 3 h a y x = y = z = 3
Vậy giá trị nhỏ nhất của P là 3 3 2

\(\dfrac{1}{x}+\dfrac{2}{y}\le1\Rightarrow\dfrac{2}{y}\le1-\dfrac{1}{x}\Rightarrow y\ge\dfrac{2x}{x-1}=2+\dfrac{2}{x-1}\)
\(x+\dfrac{2}{z}\le3\Rightarrow x< 3;\dfrac{2}{z}\le3-x\Rightarrow z\ge\dfrac{2}{3-x}\Rightarrow y+z\ge2+\dfrac{2}{x-1}+\dfrac{2}{3-x}\)
Lúc này ta sẽ áp dụng bất đẳng thức Bunhiacopski
Ta có:
\(6^2\le\left(y+z\right)^2=\left(\sqrt{2}\dfrac{y}{\sqrt{2}}Z\right)^2\le3\left(\dfrac{y^2}{2}+z^2\right)=\dfrac{3}{2}\left(y^2+2z^2\right)\)
\(\Rightarrow P\ge24\). Dấu đẳng thức xảy ra khi và chỉ khi \(y=4,z=2\)
Vậy giá trị nhỏ nhật của P là 24
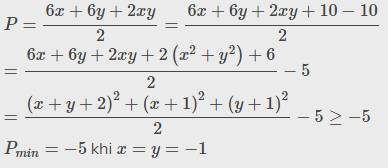

Lời giải:
$A=(x+y)(x^2-xy+y^2)+x^2+y^2=2(x^2-xy+y^2)+x^2+y^2=2(x^2+y^2)+(x-y)^2$
$\geq 2(x^2+y^2)=(1^2+1^2)(x^2+y^2)\geq (x+y)^2=2^2=4$ (theo BĐT Bunhiacopxky)
Vậy $A_{\min}=4$. Giá trị này đạt tại $x=y=1$