Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Toán lớp 0 ????? \(\text{ 🤔 }\text{ 🤔 }\text{ 🤔 }\text{ 😅 }\text{ 😅 }\text{ 😅 }\)

Đáp án D
Ta có C 12 1 . C 10 1 = 120
Khi đó C 12 1 . C 10 1 = 120 . Đặt C 12 1 . C 10 1 = 120
Ta luôn có C 12 1 . C 10 1 = 120
C 12 1 . C 10 1 = 120 Suy ra C 12 1 . C 10 1 = 120
Xét hàm số f t = t 2 − 8 t + 3 trên khoảng − 1 ; + ∞ ,có f ' t = 2 t + 1 2 t + 4 t + 3 2 > 0 ; ∀ t > − 1
Hàm số f(t) liên tục trên − 1 ; + ∞ ⇒ f t đồng biến trên − 1 ; + ∞
Do đó, giá trị nhỏ nhất của f(t) là min − 1 ; + ∞ f t = f − 1 = − 3 . Vậy P min = − 3

Đáp án C.
Ta có:
G T ⇔ 5 x + 2 y + x + 2 y − 3 − x − 2 y = 5 x y − 1 − 3 1 − x y + x y − 1.
Xét hàm số
f t = 5 t + t − 3 − t ⇒ f t = 5 t ln 5 + 1 + 3 − t ln 3 > 0 ∀ t ∈ ℝ
Do đó hàm số đồng biến trên ℝ suy ra f x + 2 y = f x y − 1 ⇔ x + 2 y = x y − 1
⇔ x = 2 y + 1 y − 1 ⇒ T = 2 y + 1 y − 1 + y . Do x > 0 ⇒ y > 1
Ta có: T = 2 + y + 3 y − 1 = 3 + y − 1 + 3 y − 1 ≥ 3 + 2 3 .

Đáp án B.
Từ giả thiết, suy ra 5 x + 2 y + 1 3 x y - 1 + x + 1 = 5 x y - 1 + 1 3 x + 2 y + x y - 2 y
⇔ 5 x + 2 y - 1 3 x + 2 y + x + 2 y = 5 x y - 1 - 1 3 x y - 1 + ( x y - 1 ) (1)
Xét hàm số f ( t ) = 5 t - 1 3 t + t trên ℝ .
Đạo hàm f ' ( t ) = 5 t . ln 5 + ln 3 3 t + 1 > 0 , ∀ t ∈ ℝ ⇒ hàm số f (t) luôn đồng biến trên ℝ .
Suy ra 1 ⇔ f ( x + 2 y ) = f ( x y - 1 ) ⇔ x + 2 y = x y - 1 ⇔ x + 1 = y ( x - 2 )
y = x + 1 x - 2
Do y > 0 nên x + 1 x - 2 > 0 ⇔ x > 2 x < - 1 . Mà x > 0 nên x > 2.
Từ đó T = x + y = x + x + 1 x - 2 . Xét hàm số g ( x ) = x + x + 1 x - 2 trên 2 ; + ∞ .
Đạo hàm g ' ( x ) = 1 - 3 x - 2 2 > 0 , g ' ( x ) = 0 ⇔ ( x - 2 ) 2 = 3
⇔ x = 2 + 3 ( t m ) x = 2 - 3 ( L ) . Lập bảng biến thiên của hàm số trên 2 ; + ∞ , ta thấy m i n g ( x ) = g ( 2 + 3 ) = 3 + 2 3 .
Vậy T m i n = 3 + 2 3 khi x = 2 + 3 và y = 1 + 3 .

áp án B
Ta có: log 3 x + 1 y + 1 y + 1 = 9 − x − 1 y + 1 ⇔ y + 1 log 3 x + 1 y + 1 + x − 1 y + 1 = 9
⇔ y + 1 log 3 c + 1 y + 1 + x + 1 y + 1 − 2 y = 11
⇔ y + 1 log 3 c + 1 y + 1 − 2 = 9 − x + 1 y + 1 *
Nếu x + 1 y + 1 > 9 ⇒ V T * > 0 ; V P * < 0
Ngược lại nếu x + 1 y + 1 < 9 ⇒ V T * < 0 ; V P * > 0
Do đó * ⇔ x + 1 y + 1 = 9 ⇔ x y + x + y = 8
Khi đó P = x + y 3 − 3 x y x + y − 57 x + y = x + y 3 − 3 8 − x − y x + y − 57 x + y
Đặt t = x + y ≥ 2 ⇒ f t = t 3 − 3 8 − t t − 57 t = t 3 + 3 t 2 − 81 t
⇒ f ' t = 3 t 2 + 6 t − 81 = 0 ⇒ t = − 1 + 2 7 ⇒ P min = f − 1 + 2 7 = 83 − 112 7 ⇒ a + b = − 29

Đáp án D
Cho x,y > 0 thỏa mãn 2 ( x 2 + y 2 ) + x y = ( x + y ) ( 2 + x y ) ⇔ 2 ( x + y ) 2 - ( 2 + x y ) ( x + y ) - 3 x y = 0 (*)
Đặt x + y = u x y = v ta đc PT bậc II: 2 u 2 - ( v + 2 ) u - 3 = 0 gải ra ta được u = v + 2 + v 2 + 28 v + 4 4
Ta có P = 4 ( x 3 y 3 + y 3 x 3 ) - 9 ( x 2 y 2 + y 2 x 2 ) = 4 ( x y + y x ) 3 - 9 ( x y + y x ) 2 - 12 ( x y + y x ) + 18 , đặt t = ( x y + y x ) , ( t ≥ 2 ) ⇒ P = 4 t 3 - 9 t 2 - 12 t + 18 ; P ' = 6 ( 2 t 2 - 3 t + 2 ) ≥ 0 với ∀ t ≥ 2 ⇒ M i n P = P ( t 0 ) trong đó t 0 = m i n t = m i n ( x y + y x ) với x,y thỏa mãn điều kiện (*).
Ta có :
t = ( x y + y x ) = ( x + y ) 2 x y - 2 = u 2 v - 2 = ( v + 2 + v 2 + 28 v + 4 ) 2 16 v - 2 = 1 16 ( v + 2 v + v + 4 v + 28 ) 2 - 2 ≥ 1 16 ( 2 2 + 32 ) 2 - 2 = 5 2
Vậy m i n P = P ( 5 2 ) = 4 . ( 5 2 ) 2 - 9 ( 5 2 ) 2 - 12 . 5 2 + 18 = - 23 4
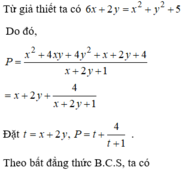
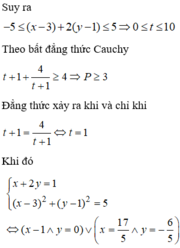
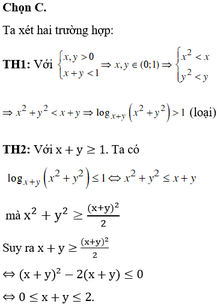
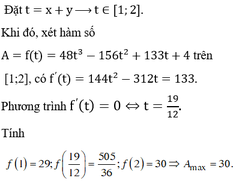
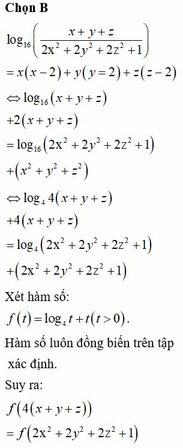


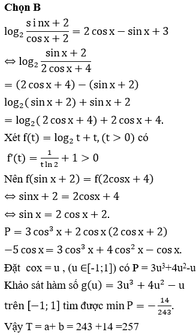
Ta có
ĐÁP ÁN C