Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: (a-1)(a-3)(a-4)(a-6)+9
=(a^2-7a+6)(a^2-7a+12)+9
=(a^2-7a)^2+18(a^2-7a)+81
=(a^2-7a+9)^2>=0
b: \(A=\dfrac{a^4-4a^3+a^2+4a^3-16a+4+16a-3}{a^2}=\dfrac{16a-3}{a^2}\)
a^2-4a+1=0
=>a=2+căn 3 hoặc a=2-căn 3
=>A=11-4căn 3 hoặc a=11+4căn 3

\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\) ; \(\forall a;b;c\)
\(\Leftrightarrow a^2+b^2+c^2\ge ab+bc+ca\)
\(\Rightarrow ab+bc+ca\le1\)
\(\Rightarrow P_{max}=1\) khi \(a=b=c\)
Lại có:
\(\left(a+b+c\right)^2\ge0\) ; \(\forall a;b;c\)
\(\Leftrightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)\ge0\)
\(\Leftrightarrow ab+bc+ca\ge-\dfrac{a^2+b^2+c^2}{2}=-\dfrac{1}{2}\)
\(P_{min}=-\dfrac{1}{2}\) khi \(a+b+c=0\)

a)Có \(a^2+1\ge2a\) với mọi a; \(b^2+1\ge2b\) với mọi b
Cộng vế với vế \(\Rightarrow a^2+b^2+2\ge2\left(a+b\right)\)
Dấu = xảy ra <=> a=b=1
b) Áp dụng BĐT bunhiacopxki có:
\(\left(x+y\right)^2\le\left(1+1\right)\left(x^2+y^2\right)\Leftrightarrow\left(x+y\right)^2\le2\)
\(\Leftrightarrow-\sqrt{2}\le x+y\le\sqrt{2}\)
\(\Rightarrow\left(x+y\right)_{max}=\sqrt{2}\Leftrightarrow\left\{{}\begin{matrix}x+y=\sqrt{2}\\x=y\end{matrix}\right.\)\(\Leftrightarrow x=y=\dfrac{\sqrt{2}}{2}\)
\(\left(x+y\right)_{min}=-\sqrt{2}\Leftrightarrow\left\{{}\begin{matrix}x+y=-\sqrt{2}\\x=y\end{matrix}\right.\)\(\Leftrightarrow x=y=-\dfrac{\sqrt{2}}{2}\)
c) \(S=\dfrac{1}{ab}+\dfrac{1}{a^2+b^2}=\dfrac{1}{a^2+b^2}+\dfrac{1}{2ab}+\dfrac{1}{2ab}\)
Với x,y>0, ta có: \(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}\) (1)
Thật vậy (1) \(\Leftrightarrow\dfrac{y+x}{xy}\ge\dfrac{4}{x+y}\Leftrightarrow\left(x+y\right)^2\ge4xy\)\(\Leftrightarrow\left(x-y\right)^2\ge0\) (lđ)
Áp dụng (1) vào S ta được:
\(S\ge\dfrac{4}{a^2+b^2+2ab}+\dfrac{1}{2ab}\)
Lại có: \(ab\le\dfrac{\left(a+b\right)^2}{4}\) \(\Leftrightarrow2ab\le\dfrac{\left(a+b\right)^2}{2}\Leftrightarrow2ab\le\dfrac{1}{2}\)\(\Rightarrow\dfrac{1}{2ab}\ge2\)
\(\Rightarrow S\ge\dfrac{4}{\left(a+b\right)^2}+2=6\)
\(\Rightarrow S_{min}=6\Leftrightarrow a=b=\dfrac{1}{2}\)

\(\left(ad+bc\right)\left(a^2d^2+b^2c^2\right)=0\)
\(\Rightarrow a^3d^3+adb^2c^2+bca^2d^2+b^3c^3=0\)
\(\Rightarrow a^3d^3+abcd\left(bc+ad\right)+b^3c^3=0\)
\(\Rightarrow a^3d^3+abcd.0+b^3c^3=0\)
\(\Rightarrow a^3d^3+b^3c^3=0\)

Bài 1: Ta có:
\(M=\frac{ad}{abcd+abd+ad+d}+\frac{bad}{bcd.ad+bc.ad+bad+ad}+\frac{c.abd}{cda.abd+cd.abd+cabd+abd}+\frac{d}{dab+da+d+1}\)
\(=\frac{ad}{1+abd+ad+d}+\frac{bad}{d+1+bad+ad}+\frac{1}{ad+d+1+abd}+\frac{d}{dab+da+d+1}\)
$=\frac{ad+abd+1+d}{ad+abd+1+d}=1$
Bài 2:
Vì $a,b,c,d\in [0;1]$ nên
\(N\leq \frac{a}{abcd+1}+\frac{b}{abcd+1}+\frac{c}{abcd+1}+\frac{d}{abcd+1}=\frac{a+b+c+d}{abcd+1}\)
Ta cũng có:
$(a-1)(b-1)\geq 0\Rightarrow a+b\leq ab+1$
Tương tự:
$c+d\leq cd+1$
$(ab-1)(cd-1)\geq 0\Rightarrow ab+cd\leq abcd+1$
Cộng 3 BĐT trên lại và thu gọn thì $a+b+c+d\leq abcd+3$
$\Rightarrow N\leq \frac{abcd+3}{abcd+1}=\frac{3(abcd+1)-2abcd}{abcd+1}$
$=3-\frac{2abcd}{abcd+1}\leq 3$
Vậy $N_{\max}=3$

a) x2 + 1 ≤ (x - 2)2 ⇔ x2 + 1 ≤ x2 - 4x + 4 ⇔ 4x ≤ 3
⇔ x ≤ 3/4
Vậy: x ≤ 3/4
b) a, b > 0
Ta có: a + b = 1 suy ra: (a + b)2 = 1 ⇒ a2 + 2ab + b2 = 1 (1)
Mặt khác (a - b)2 ≥ 0 với mọi a, b ⇒ a2 - 2ab + b2 ≥ 0 (2)
Cộng (1) và (2) vế theo vế, ta được:
2a2 + 2b2 ≥ 1 ⇒ 2(a2 + b2) ≥ 1 ⇒ a2 + b2 ≥ 1/2
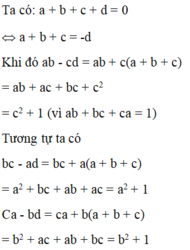

\(a^2+b^2+1=ab+b+a\)
\(\Leftrightarrow2a^2+2b^2+2-2ab-2b-2a=0\)
\(\Leftrightarrow a^2-2a+1+b^2-2b+1+a^2-2ab+b^2=0\)
\(\Leftrightarrow\left(a-1\right)^2+\left(b-1\right)^2+\left(a-b\right)^2=0\)
\(\Leftrightarrow a=b=1\)
Khi đó \(S=\left(1+\dfrac{a}{b}\right)\left(1+b\right)\left(1+\dfrac{1}{a}\right)=2.2.2=8\)