Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
+ Xét hàm y = f(x) = cos 3x
TXĐ: D = R
Với mọi x ∈ D, ta có: -x ∈ D và f(-x) = cos (-3x) = cos 3x = f(x)
Do đó, y = f(x) = cos 3x là hàm chẵn trên tập xác định của nó.
+ Xét hàm y = g(x) = sin (x2 + 1)
TXĐ: D = R
Với mọi x ∈ D, ta có: -x ∈ D và g(-x) = sin ((-x)2 + 1) = sin (x2 + 1) = g(x)
Do đó: y = g(x) = sin (x2 + 1) là hàm chẵn trên R.
+ Xét hàm y = h(x) = tan2 x
TXĐ: D = R\{π/2 + k2π, k ∈ Z)
Với mọi x ∈ D, ta có: -x ∈ D và h(-x) = tan2 (-x) = tan2 x = h(x)
Do đó: y = h(x) = tan2 x là hàm số chẵn trên D
+ Xét hàm y = t(x) = cot x.
TXĐ: D = R\{kπ, k ∈ Z)
Với mọi x ∈ D, ta có: -x ∈ D và t(-x) = cot (-x) = -cot x = -t(x)
Do đó: y = t(x) = cot x là hàm số lẻ trên D.

a.
\(y'=\dfrac{3}{cos^2\left(3x-\dfrac{\pi}{4}\right)}-\dfrac{2}{sin^2\left(2x-\dfrac{\pi}{3}\right)}-sin\left(x+\dfrac{\pi}{6}\right)\)
b.
\(y'=\dfrac{\dfrac{\left(2x+1\right)cosx}{2\sqrt{sinx+2}}-2\sqrt{sinx+2}}{\left(2x+1\right)^2}=\dfrac{\left(2x+1\right)cosx-4\left(sinx+2\right)}{\left(2x+1\right)^2}\)
c.
\(y'=-3sin\left(3x+\dfrac{\pi}{3}\right)-2cos\left(2x+\dfrac{\pi}{6}\right)-\dfrac{1}{sin^2\left(x+\dfrac{\pi}{4}\right)}\)
+ Xét hàm số y= f(x) = cos3x
TXĐ: D =R
Với mọi x ∈ D , ta có: - x ∈ D và
f( -x) = cos( - 3x) = cos3x = f(x)
Do đó, y= cos 3x là hàm chẵn trên tập xác định của nó.
+ Xét hàm y= g(x)= sin(x2 + 1)
TXĐ: D= R
Với mọi x ∈ D , ta có: - x ∈ D và
g( -x)= sin[ (-x)2 +1]= sin( x2+1)= g(x)
Do đó: y= sin( x2 +1) là hàm chẵn trên R.
+ Xét hàm số y= h( x)= tan2x .
TXĐ: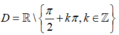
Với mọi x ∈ D , ta có: - x ∈ D và
h( -x)= tan2 (-x)= (- tanx)2 = tan2 x= h(x)
Do đó y= tan2x là hàm số chẵn trên D.
+ Xét hàm số y= t(x)= cotx.
TXĐ: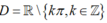
Với mọi x ∈ D , ta có: - x ∈ D và t(-x)= cot(-x) = - cotx = - t(x)
Do đó: y= cotx là hàm số lẻ trên D.
Vậy (1); (2); (3) là các hàm số chẵn
Đáp án C