Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác đều ABC diện tích 80 cm2. Dựng một tam giác vuông cân BCD như hình vẽ.

Sau đó lại lấy cạnh BD của tam giác vuông cân để dựng một tam giác đều. Cứ lặp đi lặp lại như vậy đến tam giác đều thứ 4.
Hỏi tam giác đều thứ 4 có diện tích bằng bao nhiêu?
Đáp án: 10 cm2.
Gọi cạnh tam giác đều ABC là a.
Áp dụng định lý Pytago vào tam giác vuông cân BCD ta có BD = CD = a√2/2
Nhận thấy, BD chính là cạnh của tam giác đều tiếp theo. Từ đó suy ra cạnh của tam giác đều tiếp theo luôn giảm √2/2 lần so với cạnh của tam giác đều trước đó.
Suy ra cạnh của tam giác đều thứ 4 giảm (√2/2)3 = √2/4 lần so với cạnh tam giác đầu tiên. Từ đây ta có diện tích tam giác đều thứ tư bằng (√2/4)2 = 1/8 lần so với diện tích tam giác đều đầu tiên.
Vậy diện tích tam giác đều thứ 4 bằng 80/8 = 10 cm2.

* Xét tam giác ABC có D và E lần lượt là trung điểm của AB và AC nên DE là đường trung bình của tam giác.
Suy ra: DE// BC và
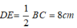
* Xét tứ giác DECB có DE // BC nên DECB là hình thang.
Lại có: M và N lần lượt là trung điểm của BD và EC nên MN là đường trung bình của hình thang .

Chọn đáp án D
Lời giải:
a) Vì $FN\parallel AC$ nên áp dụng định lý Talet:
\(\frac{NC}{NB}=\frac{FA}{FB}=\frac{DB}{DC}\)
Nếu $NB=DC$ thì do $MB=MC$ nên $MB-NB=MC-DC$
$\Leftrightarrow MN=MD$ nên $M$ là trung điểm $DN$.
Nếu $NB\neq DC$ thì áp dụng TCDTSBN: $\frac{NC}{NB}=\frac{DB}{DC}=\frac{NC-DB}{NB-DC}=\frac{DC-NB}{NB-DC}=-1< 0$ (vô lý)
Vậy ta có đpcm.
b)
Vì $M$ là trung điểm $DN$, $P$ là trung điểm $DF$ nên $MP$ là đtb ứng với cạnh $FN$
$\Rightarrow MP\parallel FN$ và $MP=\frac{1}{2}FN(1)$
Mặt khác:
$FN\parallel AC\Rightarrow FN\parallel AE(2)$
$\frac{NC}{NB}=\frac{FA}{FB}=\frac{EC}{EA}$ nên theo Talet đảo thì $EN\parallel AB$ hay $EN\parallel AF(3)$
Từ $(2); (3)$ suy ra $AENF$ là hình bình hành nên $AE=FN(4)$
Từ $(1); (2);(4)$ suy ra $MP\parallel AE$ và $MP=\frac{1}{2}AE$ (đpcm)
c) Gọi $G$ là giao điểm $AM$ và $EP$. Theo định lý Talet:
$\frac{AG}{GM}=\frac{EG}{GP}=\frac{AE}{MP}=2$
$\Rightarrow \frac{AG}{AM}=\frac{EG}{EP}=\frac{2}{3}$
Do đó $G$ chính là trọng tâm của $ABC$ và $DEF$. Ta có đpcm.
Hình vẽ: