Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chiều cao AH của tứ diện ABCD chính là khoảng cách từ điểm A đến mp (BCD) :
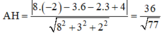
a) Cách 1:
Phương trình đoạn chắn (ABC) là:
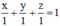hay x + y + z – 1 = 0.
Thay tọa độ điểm D(-2; 1; -1) ta được: (-2) + 1 + (-1) – 1 = -3 ≠ 0
⇒ D không nằm trong (ABC)
⇒ A, B, C, D không đồng phẳng
⇒ A, B, C, D là bốn đỉnh của một tứ diện.
Cách 2:
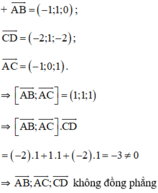
⇒ A, B, C, D không đồng phẳng
⇒ A, B, C, D là bốn đỉnh của hình tứ diện.
Phương trình đường thẳng SB: x - t, y = 2t, z = 2 - 2t. Để tìm B' ta giải hệ
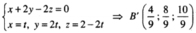
Tương tự, C'(0; 1; 1)
\(\overrightarrow{AB}=\left(1;2;3\right)\) ; \(\overrightarrow{CD}=\left(1;1;1\right)\)
\(\left[\overrightarrow{AB};\overrightarrow{CD}\right]=\left(-1;2;-1\right)=-\left(1;-2;1\right)\)
Phương trình (P):
\(1\left(x-1\right)-2y+1\left(z-1\right)=0\Leftrightarrow x-2y+z-2=0\)
Để tìm phương trình mặt phẳng (P) ta cần tìm được vector pháp tuyến của mặt phẳng. Vì mặt phẳng (P) song song với đường thẳng AB nên vector pháp tuyến của (P) cũng vuông góc với vector chỉ phương của AB, tức là AB(1-0;2-0;4-1)=(1;2;3).
Vì (P) đi qua C(1;0;1) nên ta dễ dàng tìm được phương trình của (P) bằng cách sử dụng công thức phương trình mặt phẳng:
3x - 2y - z + d = 0, trong đó d là vế tự do.
Để tìm d, ta chỉ cần thay vào phương trình trên cặp tọa độ (x;y;z) của điểm C(1;0;1):
3(1) -2(0) - (1) + d = 0
⇒ d = -2
Vậy phương trình của mặt phẳng (P) là:
3x - 2y - z - 2 = 0,
và đáp án là B.
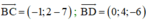
(BCD) nhận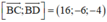 
là 1 vtpt
⇒ (BCD): 16x – 6y – 4z + 8 = 0
hay (BCD): 8x – 3y – 2z + 4 = 0.
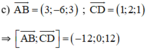
(α) chứa AB và song song với CD
⇒ (α) nhận (1; 0; -1) là 1 vtpt
(α) đi qua A(-2; 6; 3)
⇒ (α): x – z + 5 = 0.
Chọn B
Mặt phẳng (ABC) đi qua B (1; 0; -1) và có một véctơ pháp tuyến là:
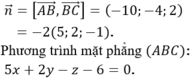
Phương trình mặt phẳng (ABC): 5x + 2y - z - 6 = 0
Độ dài đường cao xuất phát từ đỉnh D (0; 0; d) của tứ diện ABCD bằng d(D, (ABC))
Theo bài ra ta có:
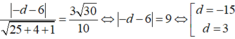
Do D thuộc tia Oz nên D (0; 0; 3).
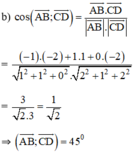
Độ dài đường cao hình chóp A.BCD chính là khoảng cách từ A đến (BCD).
⇒ (BCD) nhận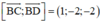
là 1 vtpt
⇒ (BCD): x – 2y – 2z + 2 = 0
⇒ Độ dài đường cao hình chóp A.BCD là: