PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
6 tháng 7 2018
a) Thay phân thức P vào biểu thức A rồi rút gọn chúng ta thu được A = u + v với điều kiện các biểu thức có nghĩa.
b) Tương tự a) ta có B = 1.
15 tháng 9 2019
Thay P = \(\frac{xy}{x-y}\) vào biểu thức ta được :
\(\frac{x.\frac{xy}{x-y}}{x+\frac{xy}{x-y}}-\frac{y.\frac{xy}{x-y}}{y-\frac{xy}{x-y}}\)
Ta có :
\(\frac{x.\frac{xy}{x-y}}{x+\frac{xy}{x-y}}=\frac{x^2y}{x-y}:\left(x+\frac{xy}{x-y}\right)\)
= \(\frac{x^2y}{x-y}:\frac{x\left(x-y\right)+xy}{x-y}\)
= \(\frac{x^2y}{x-y}:\frac{x^2}{x-y}\)
= \(\frac{x^2y}{x-y}.\frac{x-y}{x^2}\)
= \(y\)
\(\frac{y.\frac{xy}{x-y}}{y-\frac{xy}{x-y}}=\frac{xy^2}{x-y}:\left(y-\frac{xy}{x-y}\right)\)
= \(\frac{xy^2}{x-y}:\frac{y\left(x-y\right)-xy}{x-y}\)
= \(\frac{xy^2}{x-y}:\frac{-y^2}{x-y}\)
= \(\frac{xy^2}{x-y}.\frac{x-y}{-y^2}\)
= \(-x\)
Vậy giá trị biểu thức bằng \(y-\left(-x\right)=x+y\)
Chúc bạn học tốt !!!
17 tháng 4 2021
\(\dfrac{x^2-4x+4}{x^3-2x^2-\left(4x-8\right)}=\dfrac{\left(x-2\right)^2}{x^3-2x^2-4x+8}\)
Để biểu thức trên nhận giá trị âm khi \(\dfrac{\left(x-2\right)^2}{x^3-2x^2-4x+8}< 0\)
\(\Rightarrow x^3-2x^2-4x+8< 0\)do \(\left(x-2\right)^2\ge0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-2x+4\right)-2x\left(x+2\right)< 0\)
\(\Leftrightarrow\left(x+2\right)\left(x-2\right)^2< 0\Leftrightarrow x< -2\)
CD
0
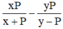
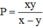
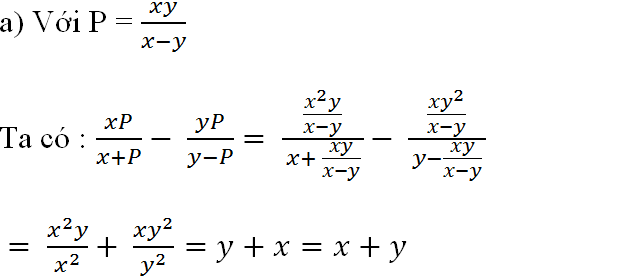
Thay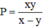
vào biểu thức ta được:
Ta có:
Vậy giá trị biểu thức bằng y – (-x) = x + y.