
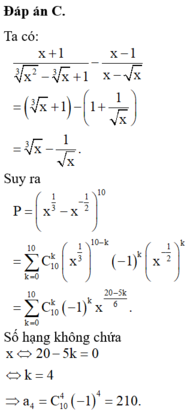
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

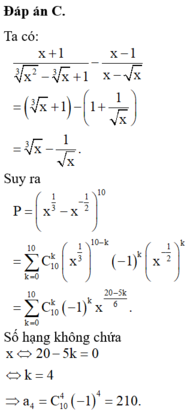

Chọn A
Số hạng tổng quát của biểu thức
x
-
2
x
2
21
,
x
≠
0
khi khai triển theo công thức nhị thức Newton là 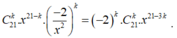
Số hạng không chứa x trong khai triển nhị thức Newton
x
-
2
x
2
21
,
x
≠
0
là ![]() với k thỏa mãn
với k thỏa mãn
21-3k = 0 => k = 7
Vậy số hạng không chứa x trong khai triển nhị thức Newton
x
-
2
x
2
21
,
x
≠
0
là ![]()

\(P=\left(\frac{\left(\sqrt[3]{x}+1\right)\left(\sqrt[3]{x^2}-\sqrt[3]{x}+1\right)}{\sqrt[3]{x^2}-\sqrt[3]{x}+1}-\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\right)^{10}\)
\(=\left(\sqrt[3]{x}+1-\frac{\sqrt{x}+1}{\sqrt{x}}\right)^{10}=\left(\sqrt[3]{x}-\frac{1}{\sqrt{x}}\right)^{10}=\left(x^{\frac{1}{3}}-x^{\frac{-1}{2}}\right)^{10}\)
\(=\sum\limits^{10}_{k=0}C_{10}^k.\left(-1\right)^{10-k}.\left(x^{\frac{1}{3}}\right)^k.\left(x^{\frac{-1}{2}}\right)^{10-k}=\sum\limits^{10}_{k=0}C_{10}^k\left(-1\right)^{10-k}x^{\frac{5k-30}{6}}\)
Số hạng ko chứa x \(\Rightarrow\frac{5k-30}{6}=0\Rightarrow k=6\)
\(\Rightarrow C_{10}^6.\left(-1\right)^4=210\)

Chọn C
Số hạng tổng quát trong khai triển 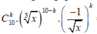
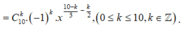 .
.
Số hạng không chứa x ứng với k thỏa mãn: 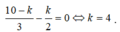 .
.
Vậy số hạng không chứa x cần tìm: ![]() .
.