Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

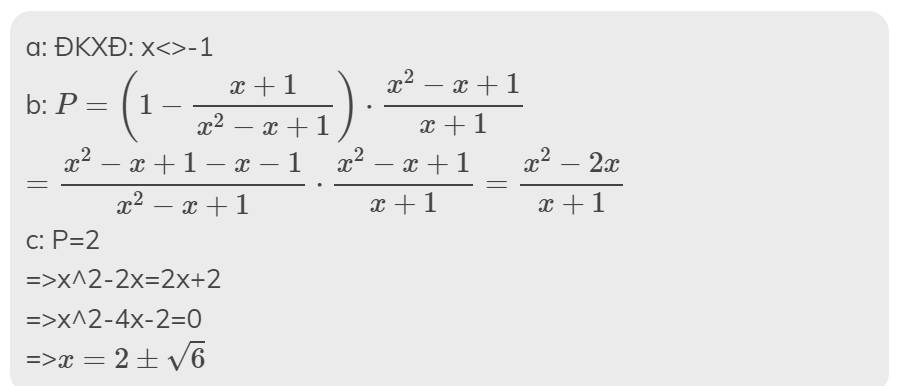
a: ĐKXĐ: x<>-1
b: \(P=\left(1-\dfrac{x+1}{x^2-x+1}\right)\cdot\dfrac{x^2-x+1}{x+1}\)
\(=\dfrac{x^2-x+1-x-1}{x^2-x+1}\cdot\dfrac{x^2-x+1}{x+1}=\dfrac{x^2-2x}{x+1}\)
c: P=2
=>x^2-2x=2x+2
=>x^2-4x-2=0
=>\(x=2\pm\sqrt{6}\)

a, điều kiện xác định: x2 - 4 ≠ 0
⇔ x2 ≠ 4
⇔x ≠ 2 và x ≠ -2
b, A= \(\dfrac{x^2}{x^2-4}-\dfrac{x}{x-2}+\dfrac{2}{x+2}\)
=\(\dfrac{x^2-x\left(x+2\right)+2\left(x-2\right)}{x^2-4}\)
= \(\dfrac{x^2-x^2-2x+2x-4}{x^2-4}\)
= \(\dfrac{x^2-4}{x^2-4}\)
= 1
c, x=1 ⇒ A= \(\dfrac{1^2}{1^2-4}-\dfrac{1}{1-2}+\dfrac{2}{1+2}\)
= \(\dfrac{4}{3}\)
a) Điều kiện xác định:
A\(\left\{{}\begin{matrix}x-2\ne0\\x+2\ne0\end{matrix}\right.⇔\left\{{}\begin{matrix}x\ne2\\x\ne-2\end{matrix}\right.\)
b) Rút gọn:
A= \(\dfrac{x^2}{x^2-4}-\dfrac{x}{x-2}+\dfrac{2}{x+2}\).
A= \(\dfrac{x^2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x}{x-2}+\dfrac{2}{x+2}\).
A= \(\dfrac{x^2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}+\dfrac{2\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)[do MTC là (x-2)(x+2)].
A= \(\dfrac{x^2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x^2+2x}{\left(x-2\right)\left(x+2\right)}+\dfrac{2x-4}{\left(x-2\right)\left(x+2\right)}\)
A= \(\dfrac{x^2-\left(x^2+2x\right)+2x-4}{\left(x-2\right)\left(x+2\right)}\)
A= \(\dfrac{x^2-x^2-2x+2x-4}{\left(x-2\right)\left(x+2\right)}\)
A= \(\dfrac{-4}{\left(x-2\right)\left(x+2\right)}\)

a: ĐKXĐ: \(x\notin\left\{0;1;-1\right\}\)
b: \(A=\dfrac{x\left(x+1\right)^2}{x\left(x+1\right)\left(x-1\right)}=\dfrac{x+1}{x-1}\)
c: Thay x=2 vào A, ta được:
\(A=\dfrac{2+1}{2-1}=3\)
d: Để A=2 thì x+1=2x-2
=>-x=-3
hay x=3(nhận)

a) \(A=\dfrac{x^2-4x+4}{5x-10}.\) ĐK: \(x\ne2.\)
b) \(A=\dfrac{x^2-4x+4}{5x-10}=\dfrac{\left(x-2\right)^2}{5\left(x-2\right)}=\dfrac{x-2}{5}.\)
c) \(Thay\) \(x=-2018:\) \(\dfrac{-2018-2}{5}=-404.\)

\(a,ĐK:x\ne\pm2\\ b,A=\dfrac{x^2+4x+4+x^2-4x+4+16}{2\left(x-2\right)\left(x+2\right)}\\ A=\dfrac{2x^2+32}{2\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+16}{x^2-4}\\ c,A=-3\Leftrightarrow-3x^2+12=x^2+16\\ \Leftrightarrow4x^2=-4\Leftrightarrow x\in\varnothing\)

bài1 A=\(\left(\frac{3-x}{x+3}\cdot\frac{x^2+6x+9}{x^2-9}+\frac{x}{x+3}\right):\frac{3x^2}{x+3}\)
=\(\left(-\frac{x-3\cdot\left(x+3\right)^2}{\left(x+3\right)^2\cdot\left(x-3\right)}+\frac{x}{x+3}\right):\frac{3x^2}{x+3}\)
=\(-\frac{x}{x+3}\cdot\frac{x+3}{3x^2}=\frac{-1}{3x}\)
b) thế \(x=-\frac{1}{2}\)vào biểu thức A
\(-\frac{1}{3\cdot\left(-\frac{1}{2}\right)}=\frac{2}{3}\)
c) A=\(-\frac{1}{3x}< 0\)
VÌ (-1) <0 nên 3x>0
x >0
a, ĐKXĐ: \(X\ne0;X\ne\pm1\)
b,\(A=\frac{X\left(X^2+2X+1\right)}{X\left(X^2-1\right)}=\frac{X\left(X+1\right)^2}{X\left(X-1\right)\left(X+1\right)}=\frac{X+1}{X-1}\)
c,Ta có: \(A=\frac{X+1}{X-1}=2\Leftrightarrow2\left(X-1\right)=X+1\Leftrightarrow2X-2=X+1\Leftrightarrow X=3\)
a) \(ĐKXĐ:x\ne0;x\ne1\)
b) \(A=\frac{x^3+2x^2+x}{x^3-x}\)
\(A=\frac{x\left(x^2+2x+1\right)}{x\left(x^2-1\right)}\)
\(A=\frac{x\left(x+1\right)^2}{x\left(x-1\right)\left(x+1\right)}\)
\(A=\frac{x+1}{x-1}\)
vậy \(A=\frac{x+1}{x-1}\)
c) thay vào ta được \(\frac{x+1}{x-1}=2\)
\(\Rightarrow\left(x-1\right).2=x+1\)
\(\Rightarrow2x-2=x+1\)
\(\Rightarrow2x-x=1+2\)
\(\Rightarrow x=3\)
vậy \(x=3\)thì \(A=2\)