Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các khẳng định đúng là: (1) ; (2); (3)
(4) cần sửa thành: Phương sai là bình phương của độ lệch chuẩn.
Chọn C

Số 2 lớn hơn mọi giá trị khác của hàm số f(x) = sinx với tập xác định D = R nhưng 2 không phải là giá trị lớn nhất của hàm số này (giá trị lớn nhất là 1); vì vậy A sai. Cũng như vậy B sai với f(x) = sinx, D = R, M = 2. Phát biểu C tự mâu thuẫn: vì M = f( x 0 ), x 0 ∈ D nên hay không xảy ra M > f(x), ∀x ∈ D.
Đáp án: D

Ta có:
f x = x - x 2 = - x 2 - x = - x 2 - 2 . x . 1 2 + 1 4 + 1 4 = - x - 1 2 2 + 1 4 ≤ 1 4 ∀ x
Do đó, hàm số f x = x - x 2 có giá trị lớn nhất là 1 4 khi x = 1 2 .

Tích vô hướng của hai vec tơ a→ và b→:
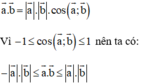
+ a→.b→ đạt giá trị lớn nhất bằng 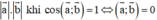 ⇔ a→ và b→ cùng hướng.
⇔ a→ và b→ cùng hướng.
+ a→.b→ đạt giá trị nhỏ nhất bằng 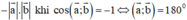 ⇔ a→ và b→ ngược hướng.
⇔ a→ và b→ ngược hướng.

c1:áp dụng bđt AM-GM:
\(a+b\ge2\sqrt{ab}\Rightarrow ab\le\left(\dfrac{a+b}{2}\right)^2=1008^2\)
=> đáp án A
c2: tương tự c1 . đáp án b
3.
\(\dfrac{a}{b}+\dfrac{b}{a}\ge2\sqrt{\dfrac{ab}{ab}}=2\)
Đáp án A
4.
\(a^2-a+1=\left(a-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\) ;\(\forall a\)
Đáp án A

Với \(a\ne0\) từ đề bài ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=2\\4a+2b+c=1\\16a+4b+c=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}4a+b=0\\4a+2b+c=1\\16a+4b+c=-3\end{matrix}\right.\)
\(\Rightarrow a=-1;b=4;c=-3\)
Vậy (P): \(y=-x^2+4x-3\)
Vì a + b = 3 nên b = 3 - a . Do đó:
a b = a 3 - a = - a 2 + 3 a = - a 2 - 2 . 3 2 a + 9 4 + 9 4 = - a - 3 2 2 + 9 4 ≤ 9 4 ∀ a
a b = 9 4 ⇔ a = b = 3 2 Vậy giá trị lớn nhất của a.b là 9 4 (đạt được khi a = b = 3 2 ).
Đáp án là B.