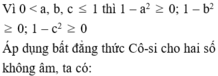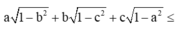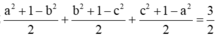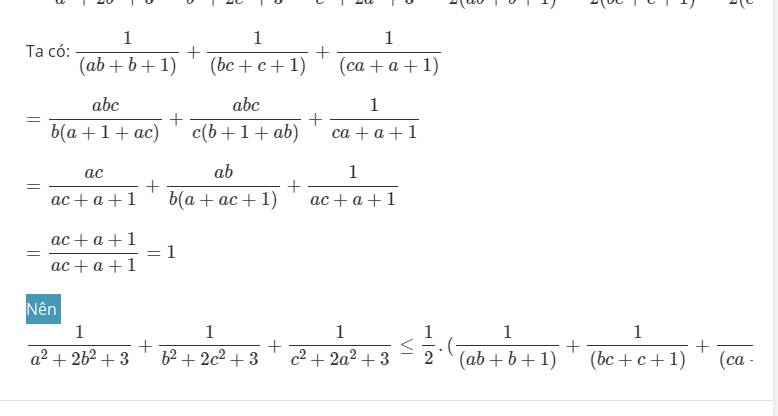Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có \(a\sqrt{1-b^2}=\sqrt{a^2\left(1-b^2\right)}\le\dfrac{a^2+1-b^2}{2}\)
\(b\sqrt{1-c^2}=\sqrt{b^2\left(1-c^2\right)}\le\dfrac{b^2+1-c^2}{2}\)
\(c\sqrt{1-a^2}=\sqrt{c^2\left(1-a^2\right)}\le\dfrac{c^2+1-a^2}{2}\)
=> \(a\sqrt{1-b^2}+b\sqrt{1-c^2}+c\sqrt{1-a^2}\le\dfrac{3}{2}\)
Dấu "=" <=> \(\left\{{}\begin{matrix}a^2=1-b^2\\b^2=1-c^2\\c^2=1-a^2\end{matrix}\right.\)
<=> \(a^2+b^2+c^2=\dfrac{3}{2}\)

\(\frac{1}{a^2+b^2+2}+\frac{1}{c^2+b^2+2}+\frac{1}{a^2+c^2+2}\le\frac{3}{4}\)
\(\Leftrightarrow\frac{a^2+b^2}{a^2+b^2+2}+\frac{b^2+c^2}{b^2+c^2+2}+\frac{c^2+a^2}{c^2+a^2+2}\ge\frac{3}{2}\)
Áp dụng BĐT Cauchy-Schwarz ta có:
\(VT\ge\frac{\left(\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\right)^2}{2\left(a^2+b^2+c^2\right)+6}\)
\(\ge\frac{\sqrt{3\left(a^2b^2+b^2c^2+c^2a^2\right)}+2\left(a^2+b^2+c^2\right)}{a^2+b^2+c^2}\)
\(\ge\frac{2\left(a^2+b^2+c^2\right)+ab+bc+ca}{a^2+b^2+c^2}\)
Cần chứng minh \(\frac{2\left(a^2+b^2+c^2\right)+ab+bc+ca}{a^2+b^2+c^2}\ge\frac{3}{2}\)
\(\Leftrightarrow\left(a+b+c\right)^2\ge0\) *luôn đúng*