Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Hoành độ giao điểm của d 1 và d 2 là nghiệm phương trình:
2x + 1 = x -1 nên x = -2
Với x = -2 thì y = 2. (-2) + 1 = -3
Vậy 2 đường thẳng d 1 và d2 cắt nhau tại A(-2; -3).
Để ba đường thẳng đã cho đồng quy thì điểm A(-2; -3) thuộc đồ thị hàm số y = (m + 1)x – 2
Suy ra: -3 = (m + 1).(-2) - 2
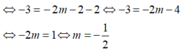

a, để (d2)//(d3)
\(< =>\left\{{}\begin{matrix}m^2+1=2\\m\ne1\end{matrix}\right.\)\(< =>m=-1\)
b, pt hoành độ giao điểm (d1)(d2)
\(x+2=2x+1< =>x=1=>y=3\)
\(pt\) hoành độ (d2)(d3)
\(2x+1=\left(m^2+1\right)x+m< =>2+1=\left(m^2+1\right)2+m\)
\(=>m=0,5\)

a) x =-2 d' => y =2(-2) -1 =-5 => M(-2;-5)
d cắt d' tại M =>k khác 2 và M thuộc (d) => k.(-2) -4 =-5 => -2k = -1 => k =1/2 (TM)
b) + Phương trình hoành độ giao điểm của d1 và d2 là:
3x =x+2 => x =1
với x =1 (d1) => y =3 => d1 cắt d2 tại N(1;3)
Để 3 đường thẳng đồng quy thì d3 qua N => (m-3).1 +2m +1 =3 => m -3 +2m +1 =3 => 3m =5 => m =5/3

* Trước hết tìm giao điểm của hai đường thẳng ( d 1 ) và ( d 2 ).
- Tìm hoành độ của giao điểm:
2/5x + 1/2 = 3/5x - 5/2 ⇔ 1/5x = 6/2 ⇔ x = 15.
- Tìm tung độ giao điểm:
y = 2/5.15 + 1/2 = 6,5.
*Tìm k (bằng cách thay tọa độ của giao điểm vào phương trình ( d 3 ).
6,5 = k.15 + 3,5 ⇔ 15k = 3 ⇔ k = 0,2.
Trả lời: Khi k = 0,2 thì ba đường thẳng đồng quy tại điểm (15; 6,5).

\(\left(d_1\right):y=-x+1\)
\(\left(d_2\right):y=x-1\)
\(\left(d_3\right):y=\dfrac{k+1}{1-k}x+\dfrac{k+1}{k-1}\)
a) Để (d1) và (d3) vuông góc với nhau:
\(\Leftrightarrow\left(-1\right)\left(\dfrac{k+1}{1-k}\right)=-1\)\(\Leftrightarrow k=0\)(thỏa)
Vậy k=0
b)Giao điểm của (d1) và (d2) là nghiệm của hệ \(\left\{{}\begin{matrix}y=-x+1\\y=x-1\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}y=0\\x=1\end{matrix}\right.\)
Để (d1);(d2);(d3) đồng quy\(\Leftrightarrow\) (d3) đi qua điểm (1;0)
\(\Rightarrow0=\dfrac{k+1}{1-k}.1+\dfrac{k+1}{k-1}\)\(\Leftrightarrow0=0\)(lđ)
Vậy với mọi k thì (d1);d2);(d3) luôn cắt nhau tại một điểm
c)Gỉa sử \(M\left(x_0;y_0\right)\) là điểm cố định mà (d3) luôn đi qua
Khi đó \(\left(k+1\right)x_0+\left(k-1\right)y_0=k+1\) luôn đúng với mọi k
\(\Leftrightarrow k\left(x_0+y_0-1\right)+x_0-y_0-1=0\) luôn đúng với mọi k
\(\Leftrightarrow\left\{{}\begin{matrix}x_0+y_0-1=0\\x_0-y_0-1=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_0=2\\y_0=1\end{matrix}\right.\)
Vậy \(M\left(2;1\right)\) là điểm cố định mà (d3) luôn đi qua.