Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

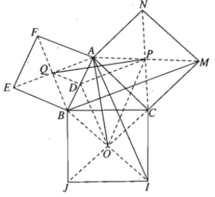
a) Phép quay tâm C góc 90 ο biến MB thành AI. Do đó MB bằng và vuông góc với AI. DP song song và bằng nửa BM, DO song song và bằng nửa AI. Từ đó suy ra DP bằng và vuông góc với DO.
b) Từ câu a) suy ra phép quay tâm D, góc 90 ο biến O thành P, biến A thành Q. Do đó OA bằng và vuông góc với PQ.

Xét phép quay tâm A góc quay 60 o biến D thành B và biến C thành E, suy ra phép quay đó biến đường thẳng DC thành đường thẳng BE suy ra góc giữa DC và BE bằng góc quay 60 o .
Chọn đáp án B.

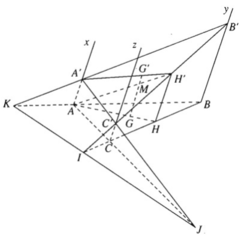
a) CC′ // BB′ ⇒ ΔICC′ ∼ ΔIBB′
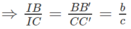
CC′ // AA′ ⇒ ΔJCC′ ∼ ΔJAA′
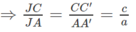
AA′ // BB′ ⇒ ΔKAA′ ∼ ΔKBB′
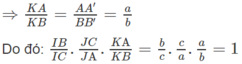
b) Gọi H và H’ lần lượt là trung điểm của các cạnh BC và B’C’. Vì HH’ là đường trung bình của hình thang BB’CC’ nên HH′ // BB′.
Mà BB′ // AA′ suy ra HH′ // AA′
Ta có: G ∈ AH và G′ ∈ A′H′ và ta có:
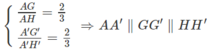
c) AH′ ∩ GG′ = M ⇒ GG′ = G′M + MG
Ta có: G′M // AA′ ⇒ ΔH′G′M ∼ ΔH′A′A
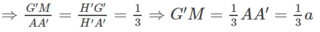
MG // HH′ ⇒ ΔAMG ∼ ΔAH′H
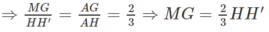
Mặt khác HH’ là đường trung bình của hình thang BB’CC’ nên
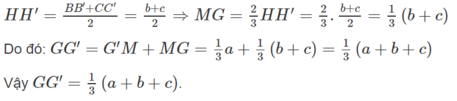

Ta dễ có tứ giác ABDE nội tiếp đường tròn đường kính AB => ^CDE = ^BAE
Lại có ^BAE = ^CAD (= 900 - ^ACB), suy ra ^CDE = ^CAD = 900 - ^ACD => DE vuông góc AC
Thấy D,E,P cùng có tung độ bằng 1 => D,E,P thẳng hàng, vì P thuộc AC nên DE vuông góc với AC tại P
Đường thẳng AC: đi qua P(2;1), VTPT \(\overrightarrow{DE}=\left(5;0\right)\) \(\Rightarrow AC:x-2=0\)
Xét hệ: \(\hept{\begin{cases}x-2=0\\x+y-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=0\end{cases}}\Rightarrow A\left(2;0\right)\)
Đường thẳng BC: đi qua \(D\left(-2;1\right)\),VTPT \(\overrightarrow{DA}=\left(4;-1\right)\Rightarrow BC:4x-y+9=0\)
Xét hệ: \(\hept{\begin{cases}x-2=0\\4x-y+9=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=17\end{cases}\Rightarrow C\left(2;17\right)}\)
Đường thẳng BE: đi qua \(E\left(3;1\right)\), VTPT \(\overrightarrow{AE}=\left(1;1\right)\Rightarrow BE:x+y-4=0\)
Xét hệ: \(\hept{\begin{cases}4x-y+9=0\\x+y-4=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=5\end{cases}}\Rightarrow B\left(-1;5\right)\)
Vậy \(A\left(2;0\right),B\left(-1;5\right),C\left(2;17\right)\).

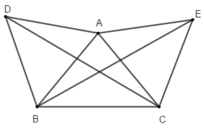
Xét phép quay tâm B góc quay -600 biến A thành D, biến E thành C suy ra phép quay này biến đoạn thẳng AE thành đoạn thẳng DC, suy ra nó biến trung điểm F của AE thành trung điểm G của DC, suy ra nó biến đoạn thẳng BF thành đoạn thẳng BG do đó BF = BG và góc FBG bằng 600. Vậy tam giác BFG là tam giác đều.
Đáp án D