Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


B=\(\frac{12}{2^2.4^2}+\frac{20}{4^2.6^2}+......+\frac{388}{96^2.98^2}+\frac{396}{98^2.100^2}\)
=\(\frac{1}{2^2}-\frac{1}{4^2}+\frac{1}{4^2}-\frac{1}{6^2}+...+\frac{1}{96^2}-\frac{1}{98^2}+\frac{1}{98^2}-\frac{1}{100^2}\)
=\(\frac{1}{2^2}-\frac{1}{100^2}\)
=\(\frac{2599}{10000}< \frac{2500}{10000}=\frac{1}{4}\)
=> B<\(\frac{1}{4}\)

\(\frac{3}{2\cdot4}+\frac{3}{4\cdot6}+\frac{3}{6\cdot8}+...+\frac{3}{96\cdot98}\)
\(=\frac{3}{2}\cdot\left(\frac{2}{2\cdot4}+\frac{2}{4\cdot6}+\frac{2}{6\cdot8}+...+\frac{2}{96\cdot98}\right)\)
\(=\frac{3}{2}\cdot\left(\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+\frac{1}{6}-\frac{1}{8}+...+\frac{1}{96}-\frac{1}{98}\right)\)
\(=\frac{3}{2}\cdot\left(\frac{1}{2}-\frac{1}{98}\right)=\frac{3}{2}\cdot\left(\frac{48}{98}-\frac{1}{98}\right)\)
\(=\frac{3}{2}\cdot\frac{47}{98}=\frac{141}{196}\)

\(B=\frac{12}{\left(2.4\right)^2}+\frac{20}{\left(4.6\right)^2}+............+\frac{388}{\left(96.98\right)^2}+\frac{396}{\left(98.100\right)^2}\)
\(B=\frac{4^2-2^2}{\left(2.4\right)^2}+\frac{6^2-4^2}{\left(4.6\right)^2}+..........+\frac{98^2-96^2}{\left(96.98\right)^2}+\frac{100^2-98^2}{\left(98.100\right)^2}\)
\(B=\frac{1}{2^2}-\frac{1}{4^2}+\frac{1}{4^2}-...............-\frac{1}{98^2}+\frac{1}{98^2}-\frac{1}{100^2}\)
\(B=\frac{1}{2^2}-\frac{1}{100^2}\)
\(B=\frac{1}{4}-\frac{1}{10000}\)
\(B=\frac{2500}{10000}-\frac{1}{10000}\)
\(B=\frac{2499}{10000}\)
Vậy B = \(\frac{2499}{10000}\)

\(A=2\times4+4\times6+6\times8+...+98\times100\)
\(6\times A=2\times4\times6+4\times6\times\left(8-2\right)+6\times8\times\left(10-4\right)+...+98\times100\times\left(102-96\right)\)
\(=2\times4\times6+4\times6\times8-2\times4\times6+6\times8\times10-4\times6\times8+...+98\times100\times102-96\times98\times100\)
\(=98\times100\times102\)
\(\Leftrightarrow A=\frac{98\times100\times102}{6}=166600\)
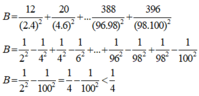
B=\(\frac{12}{\left(2.4\right)^2}\)+\(\frac{20}{\left(4.6\right)^2}\)+.....+\(\frac{396}{\left(98.100\right)^2}\)
B=\(\frac{4^2-2^2}{2^2.4^2}\)+ \(\frac{6^2-4^2}{4^2.6^2}\)+....+\(\frac{100^2-98^2}{\left(98^2.100^2\right)}\)
B=\(\frac{1}{2^2}\)-\(\frac{1}{4^2}\)+\(\frac{1}{4^2}\)-\(\frac{1}{6^2}\)+....+\(\frac{1}{98^2}\)-\(\frac{1}{100^2}\)
B=\(\frac{1}{2^2}\)-\(\frac{1}{100^2}\)< \(\frac{1}{2^2}\)=\(\frac{1}{4}\)
Vậy B<\(\frac{1}{4}\)
B<\(\frac{1}{4}\)