K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 9 2021
a: \(A=2019\cdot2021=2020^2-1\)
\(B=2020^2\)
Do đó: A<B
HN
10 tháng 10 2021
Fhzhizuu8zìtcùbìgìvìg⁸fu7fdjhtvfghhhujfghfhgkffztdhcvvgoh. Gtvguvvhhvhvzcgctv
BD
0
OY
20 tháng 7 2021
A=3+32+33+...+3100
3A=32+33+...+3101
3A-A=(32+33+...+3101)-(3+32+33+...+3100)
2A=3101-3
2A+3=3101
DX
20 tháng 7 2021
\(A=3+3^2+3^3+...+3^{100}\)
\(\Rightarrow3A=3.\left(3+3^2+3^3+...+3^{100}\right)\)
\(\Rightarrow3A=3^2+3^3+3^4+...+3^{101}\)
\(\Rightarrow3A-A=2A=\left[3^2+3^3+3^4+...+3^{101}\right]-\left[3+3^2+3^3+...+3^{100}\right]\)\(\Rightarrow2A=3^{101}-3\)
Theo đề bài ta có 2A + 3 = 3n ( \(n\in N\) )
\(\Rightarrow2A+3=3^{101}-3+3=3^n\)
\(\Rightarrow2A+3=3^{101}=3^n\)
\(\Rightarrow3^{101}=3^n\)
\(\Rightarrow101=n\) ( thỏa mãn điều kiện \(n\in N\)
Vậy n = 101
PT
1
CM
22 tháng 11 2018
Ta có: A = 3 + 3 2 + 3 3 + . . . + 3 100
=> 3 A = 3 2 + 3 3 + 3 4 + . . . + 3 101
=> 3 A - A = ( 3 2 + 3 3 + 3 4 + . . . + 3 101 ) - ( 3 + 3 2 + 3 3 + . . . + 3 100 )
=> 2 A = 3 2 + 3 3 + 3 4 + . . . + 3 101 - 3 - 3 2 - 3 3 - . . . - 3 100
2 A = 3 101 - 3 <=> 2 A + 3 = 3 101 , mà 2 A + 3 = 3 n
=> n = 101
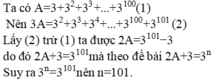
Ta có: \(B=3+3^2+3^3+3^4+...+3^n\)
\(\Leftrightarrow3B=3^2+3^3+3^4+...+3^n+3^{n+1}\)
\(\Leftrightarrow3B-B=3^{n+1}-3\)
\(\Leftrightarrow2B=3^{n+1}-3\)
mà \(B=3280\) \(\Rightarrow2B=2.3280=6560\)
\(\Rightarrow3^{n+1}-3=6560\)
\(\Leftrightarrow3^{n+1}=6560+3=6563\)
\(\Leftrightarrow3^n.3=6563\)
\(\Leftrightarrow3^n=6563:3=\frac{6563}{3}\)
\(\Rightarrow n\notin N\)
Vậy: ko tìm được \(n\in N\)
@Phạm anh quyên - Bạn xem đề bài có vấn đề gì ko, vì ko tìm được kết quả