Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

các bài toán bên dưới đều có thể áp dụng bđt tổng quát sau:
a²/x + b²/y + c²/z + d²/t ≥ (a+b+c+d)² /(x+y+z+t) (*-*)
bao nhiêu cặp số cũng đc trong đó có đk x, y, z, t > 0
dấu "=" khi a/x = b/y = c/z = d/y
~ ~ ~ ~
chứng minh là hệ quả trực tiếp từ bđt Bunhiacopski
hoặc cách khác: với 2 cặp số: a²/x + b²/y ≥ (a+b)²/(x+y)
ta chứng minh bằng biến đổi tương đương sẽ bđt đúng là (ay-bx)² ≥ 0
ad: a²/x + b²/y + c²/z ≥ (a+b)²/(x+y) + c²/z ≥ (a+b+c)²/(x+y+z)
cứ bổ sung thêm vào ta cm được cho 4, 5... cặp số
~ ~ ~ ~
1) ad (*-*) với 5 cặp số:
1/a + 1/a + 1/b + 1/c + 1/d ≥ (5)² /(2a+b+c+d)
=> 25/(2a+b+c+d) ≤ 2/a + 1/b + 1/c + 1/d
tương tự: 25/(a+2b+c+d) ≤ 2/b + 1/a + 1/c + 1/d
25/(a+b+2c+d) ≤ 2/c + 1/a + 1/b + 1/d
25/(a+b+c+2d) ≤ 2/d + 1/a + 1/b + 1/c
cộng lại 4 bđt trên:
25.VT ≤ 5(1/a + 1/b + 1/c +1/d) = 25 => VT ≤ 1 (đpcm) ; dấu "=" khi a = b = c = d = 1
~ ~ ~ ~
2) ad bđt (*-*) với 4 cặp số:
a/(b+c) + b/(c+d) + c/(d+a) + d/(a+b) =
= a²/(ab+ac) + b²/(bc+bd) + c²/(cd+ca) + d²/(da+db) ≥
≥ (a+b+ c+d)²/(ab+ac +bc+bd + cd+ca + da+db) cần cm ≥ 2
qui đồng, khai triển rút gọ => cần cm a²+b²+c²+d² ≥ 2ca + 2db
<=> (a-c)² + (b-d)² ≥ 0 là bđt đúng => đpcm
~ ~ ~ ~
3) hình như lại ghi sai đề, thử thay a = 2, b = c = 1 có:
a/(b+2a) + b/(c+2a) + c/(a+2b) = 2/5 + 1/5 + 1/4 = 17/20 ≥ 1 (???)
~ ~ ~ ~
4) vẫn ad (*-*): dùng luôn cho 8 cặp số (hoặc tách thành vài lần kủng đc)
1/a + 3(1/b) + 4(1/c) ≥ (1+3+4)² /(a+3b+4c)
1/b + 3(1/c) + 4(1/a) ≥ (1+3+4)² /(b+3c+4a)
1/c + 3(1/a) + 4(1/b) ≥ (1+3+4)² /(c+3a+4b)
cộng lại hết:
8(1/a + 1/b + 1/c) ≥ 8²/(a+3b+4c) + 8²/(b+3c+4a) + 8²/(c+3a+4b)
=> 8²/(a+3b+4c) + 8²/(b+3c+4a) + 8²/(c+3a+4b) ≤ 8(bc+ca+ab)/abc = 8
=> 1/(a+3b+4c) + 1/(b+3c+4a) + 1/(c+3a+4b) ≤ 1/8 (đpcm)
dấu "=" khi a = b = c = 3
~ ~ ~ ~ ~
5) ad (*-*)
a/(a+2b+3c) + b/(b+2c+3a) + c/(c+2a+3b) =
= a²/(a²+2ab+3ac) + b²/(b²+2bc+3ab) + c²/(c²+2ac+3bc) ≥
≥ (a+b+c)² /(a²+b²+c² + 5ab + 5ac + 5bc)
mặt khác có bđt: a²+b²+c² ≥ ab+bc+ca
=> (a+b+c)² = a²+b²+c² + 2ab+2bc+2ca ≥ 3ab+bc+3ca
=> 2(a+b+c)² ≥ (a+b+c)² + 3ab+3bc+3ca = a²+b²+c² + 5ab+5bc+5ca
=> (a+b+c)² /(a²+b²+c² + 5ab + 5ac + 5bc) ≥ 1/2
thay vào trên ta có VT ≥ 1/2 (đpcm); dấu "=" khi a = b = c

\(B=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+\frac{1}{6^2}+\frac{1}{7^2}+\frac{1}{8^2}\)
\(\Rightarrow B=\frac{1}{2^2}+...+\frac{1}{8^2}< \frac{1}{1.2}+...+\frac{1}{7.8}\)
\(\Rightarrow\frac{1}{2^2}+...+\frac{1}{8^2}< 1-\frac{1}{2}+...+\frac{1}{7}-\frac{1}{8}\)
\(\Rightarrow\frac{1}{2^2}+...+\frac{1}{8^2}< 1-\frac{1}{8}\)
\(\Rightarrow\frac{1}{2^2}+...+\frac{1}{8^2}< \frac{7}{8}< 1\)
\(\Rightarrow B< 1\)

Ta có :B = 1 + 3 + 32 + 33 + 34 + 35 + ... + 397 + 398 + 399
= (1 + 3 + 32) + (33 + 34 + 35) + ... + (397 + 398 + 399)
= (1 + 3 + 32) + 33 . (1 + 3 + 32) +...+ 397.(1 + 3 + 32)
= 13 + 33 . 13 + ... + 397.13
= 13.(1 + 33+ ... + 397) \(⋮\)13
Vậy B\(⋮\)13 (đpcm)
Ta có : B = 1 + 3 + 32 + 33 + 34 + 35 + 36 + 37+ ... + 396 + 397 + 398 + 399
= (1 + 3 + 32 + 33) + (34 + 35 + 36 + 37) + ... + (396 + 397 + 398 + 399)
= (1 + 3 + 32 + 33) + 34.(1 + 3 + 32 + 33) + ... + 396.(1 + 3 + 32 + 33)
= 40 + 34 .40 + ... + 396. 40
= 40.(1 + 34 + .. + 396) \(⋮\)40
Vậy B \(⋮\) 40 (đpcm)
a) B=1+3+32+33+...+399
B=(1+3+32)+(33+34+35)+...+(397+398+399)
B=(1+3+32)+33(1+3+32)+...397(1+3+32)
B=13+33.13+...+397.13
B=(1+33+...+97).13
=> b chia hết cho 13
b)B=(1+3+32+33)+...+(396+397+398+399)
B=(1+3+32+33)+34(1+3+32+33)+...+396(1+3+32+33)
B=40+34.40+...+396.40
B=(1+34+...+396).40
=> B hết cho 40
Ok rồi nha:v

B=(1/4+1/5+1/6+...+1/9)+(1/10+1/11+...+1/19)
1/4+1/5+1/6+1/7+1/8+1/9>1/9+1/9+1/9+1/9+1/9+1/9=6/9>1/2
1/10+1/11+...+1/19>1/19+1/19+...+1/19=10/19>1/2
10 số
=>B>1/2+1/2=1
Vậy ta có ĐPCM
BN VÀO PHẦN CÂU HỎI TƯƠNG TỰ HOẶC BN LÊN GOOGLE MÀ TRA
CÂU TRẢ LỜI DÀI LẮM MK KO MUỐN VIẾT

Nếu n là số lẻ => n+3 là số chẵn => (n+3) (n+6) chia hết cho 2
Nếu n là số chẵn => n+6 là số chẵn => (n+3) (n+6) chia hết cho 2
=> (n+3) (n+6) chia hết cho 2 với mọi STN n
Một lần nữa xin cảm ơn bạn ( le anh tu ) nhiều .
Thank you very very much .
Kết bạn nhé .

\(C=\dfrac{-5}{7}+\dfrac{-2}{7}+\dfrac{3}{4}+\dfrac{1}{4}+\dfrac{-1}{5}=-1+1-\dfrac{1}{5}=\dfrac{-1}{5}\)

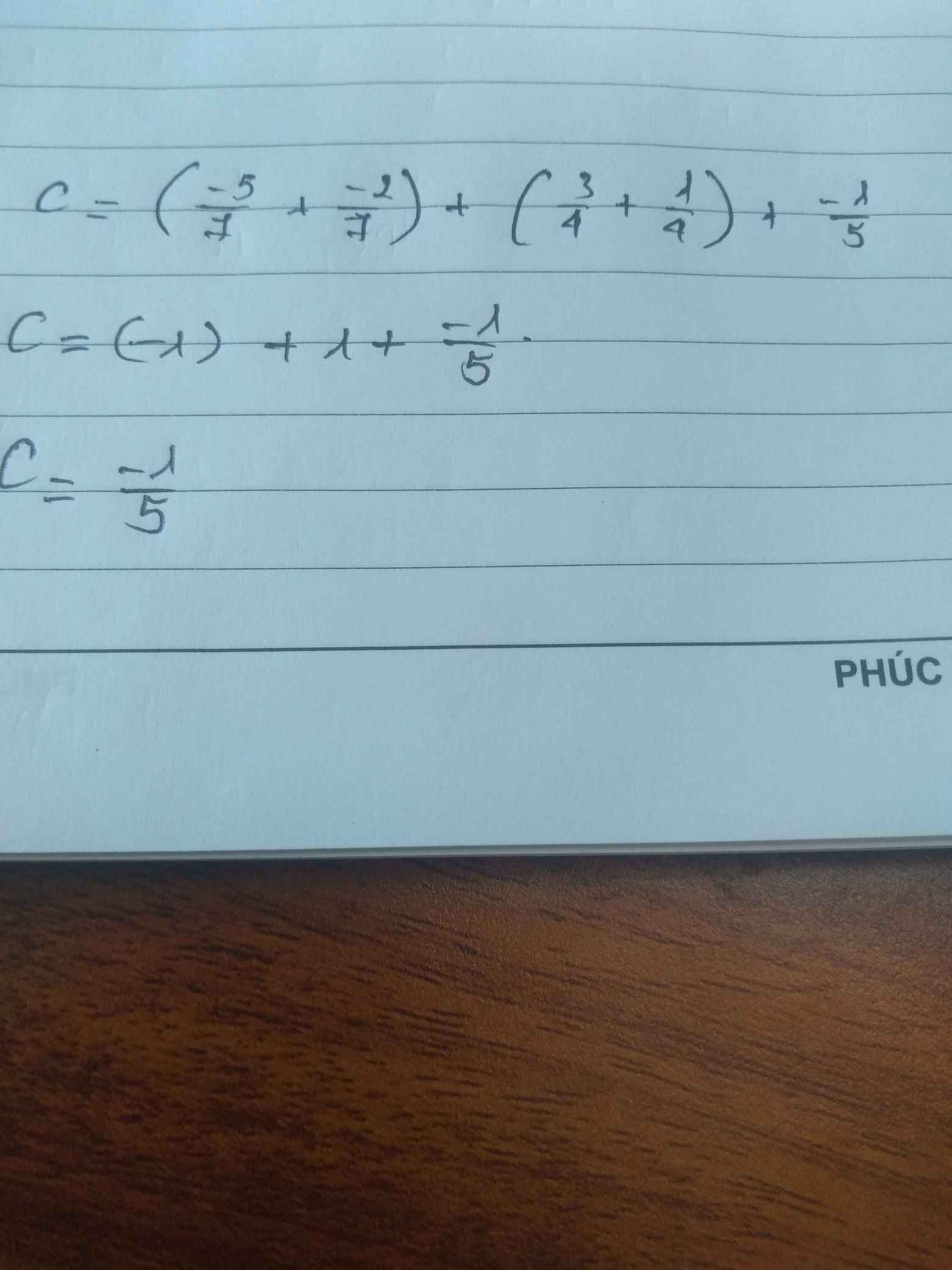
Ta có: \(\left(\dfrac{1}{4}+\dfrac{1}{5}+...+\dfrac{1}{9}\right)>\dfrac{1}{9}.6=\dfrac{6}{9}>\dfrac{1}{2}\) (1)
\(\left(\dfrac{1}{10}+\dfrac{1}{11}+...+\dfrac{1}{19}\right)>\dfrac{1}{19}.10=\dfrac{10}{19}>\dfrac{1}{2}\) (2)
\(\dfrac{1}{4}+\dfrac{1}{5}+...+\dfrac{1}{19}>\left(1\right)+\left(2\right)\)
\(\dfrac{1}{4}+\dfrac{1}{5}+...+\dfrac{1}{19}>1\left(đpcm\right)\)
gừ ... gừ sợ chưa