Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn ghi cụ thể 2 cái delta phẩy ra được không, nhìn dạng thì mới biết được
Do xét tính có nghiệm nên chỉ cần quan tâm dấu của delta phẩy, vậy chỉ cần xét dấu của 1-48bc và 1-24ac là đủ
Cộng hai cái lại ta được 2-48bc-24ac=2-24c(2b+a)
Mà a+2b+3c=1 nên 2-24c(2b+a)=2-24c(1-3c)=2-24c+72c^2
=2(1-12c+36c^2)=2(1-6c)^2 luôn không âm
Do đó ít nhất 1 trong 2 delta kia sẽ không âm

bài 2
ta có \(\left(\sqrt{8a^2+1}+\sqrt{8b^2+1}+\sqrt{8c^2+1}\right)^2\)
\(=\left(\sqrt{a}.\sqrt{\frac{8a^2+1}{a}}+\sqrt{b}.\sqrt{\frac{8b^2+1}{b}}+\sqrt{c}.\sqrt{\frac{8c^2+1}{c}}\right)^2\)\(=\left(A\right)\)
Áp dụng bất đẳng thức Bunhiacopxki ta có;
\(\left(A\right)\le\left(a+b+c\right)\left(8a+\frac{1}{a}+8b+\frac{1}{b}+8c+\frac{8}{c}\right)\)
\(=\left(a+b+c\right)\left(9a+9b+9c\right)=9\left(a+b+c\right)^2\)
\(\Rightarrow3\left(a+b+c\right)\ge\sqrt{8a^2+1}+\sqrt{8b^2+1}+\sqrt{8c^2+1}\)(đpcm)
Dấu \(=\)xảy ra khi \(a=b=c=1\)

Từ kết quả bài toán suy ngược ra thôi
Muốn giải thích thì cứ phá 2 vế ra rồi so sánh là tìm ra cách tách biểu thức
Câu 4 mình ko biết giải quyết kiểu lớp 9 (mặc dù chắc chắn là biểu thức sẽ được biến đổi như vầy)
Đó là kiểu trình bày của lớp 11 hoặc 12 để bạn tham khảo thôi

Theo bất đẳng thức Cô-Si \(a^2+\frac{1}{4}\ge a,b^2+\frac{1}{4}\ge b\to\left(a^2+b+\frac{3}{4}\right)\left(b^2+a+\frac{3}{4}\right)\)
\(\ge\left(a+b+\frac{1}{2}\right)\left(a+b+\frac{1}{2}\right)=\left(a+b+\frac{1}{2}\right)^2\) Dấu bằng xảy ra khi và chỉ khi \(a=b=\frac{1}{2}.\)
Áp dụng bất đẳng thức quen thuộc \(\left(x+y\right)^2\ge4xy,\) với \(x=a+\frac{1}{4},y=b+\frac{1}{4}\) ta được
\(\left(a+b+\frac{1}{2}\right)^2=\left(a+\frac{1}{4}+b+\frac{1}{4}\right)^2\ge4\left(a+\frac{1}{4}\right)\left(b+\frac{1}{4}\right)=\left(2a+\frac{1}{2}\right)\left(2b+\frac{1}{2}\right).\) Dấu bằng xảy ra khi và chỉ khi \(a+\frac{1}{4}=b+\frac{1}{4}\Leftrightarrow a=b.\)
Vậy vế trái lớn hơn hoặc bằng vế phải. Do đó mà các dấu bằng xảy ra, từ đây ta được \(a=b=\frac{1}{2}.\)

a) \(\frac{b-16}{4-\sqrt{b}}\left(b\ge0,b\ne16\right)\)
\(=\frac{\left(\sqrt{b}-4\right)\left(\sqrt{b}+4\right)}{4-\sqrt{b}}\)
\(=-\sqrt{b}-4\)
b) \(\frac{a-4\sqrt{a}+4}{a-4}\left(a\ge0;a\ne4\right)\)
\(=\frac{a-2.\sqrt{a}.2+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\)
\(=\frac{\left(\sqrt{a}-2\right)^2}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}=\frac{\sqrt{a}-2}{\sqrt{a}+2}\)
c) \(2x+\sqrt{1+4x^2-4x}\) với \(x\le\frac{1}{2}\)
\(=2x+\sqrt{\left(1-2x\right)^2}\)
\(=2x+\left|1-2x\right|=2x+1-2x=1\)
d) \(\frac{4a-4b}{\sqrt{a}-\sqrt{b}}\left(a,b\ge0;a\ne b\right)\)
\(=\frac{4\left(a-b\right)}{\sqrt{a}-\sqrt{b}}=\frac{4\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}\)
\(=4\left(\sqrt{a}+\sqrt{b}\right)\)

a) Giả sử bất đẳng thức trên là đúng \(\Rightarrow a^2+b^2+c^2+\frac{3}{4}+a+b+c\ge0\)\(\Rightarrow\left(a^2+a+\frac{1}{4}\right)+\left(b^2+b+\frac{1}{4}\right)+\left(c^2+c+\frac{1}{4}\right)\ge0\)(luôn đúng với mọi a,b,c), ta có ĐPCM câu b tương tự nha bn!
Bài 2:Áp dụng BĐT AM-GM ta có:
\(\frac{x}{y}+\frac{y}{z}+\frac{z}{x}\ge3\sqrt[3]{\frac{x}{y}\cdot\frac{y}{z}\cdot\frac{z}{x}}=3\)
Khi a=b=c
Bài 3:
Áp dụng BĐT C-S dạng ENgel ta có:
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{\left(1+1+1\right)^2}{a+b+c}=9\)
Khi \(a=b=c=\frac{1}{3}\)
Bài 4:
Áp dụng BĐT AM-GM ta có:
\(x+y\ge2\sqrt{xy};y+z\ge2\sqrt{yz};x+z\ge2\sqrt{xz}\)
Nhân theo vế 3 BĐT trên ta có ĐPCM
Khi x=y=z

\(1=\left(a+b+c\right)^4=\left(a^2+b^2+c^2+2\left(ab+bc+ca\right)\right)^2\)
Mặt khác áp dụng \(\left(x+y\right)^2\ge4xy\)
\(\left[\left(a^2+b^2+c^2\right)+2\left(ab+bc+ca\right)\right]^2\ge8\left(a^2+b^2+c^2\right)\left(ab+bc+ca\right)\)
\(\Rightarrow1\ge8\left(a^2+b^2+c^2\right)\left(ab+bc+ca\right)\)
\(\Rightarrow ab+bc+ca\ge8\left(a^2+b^2+c^2\right)\left(ab+bc+ca\right)^2\)
Nên ta chỉ cần chứng minh:
\(\left(ab+bc+ca\right)^2\ge a^2b^2+b^2c^2+c^2a^2\)
\(\Leftrightarrow2abc\left(a+b+c\right)\ge0\) (hiển nhiên đúng)
Đẳng thức xảy ra khi \(\left(a;b;c\right)=\left(0;0;1\right);\left(0;\dfrac{1}{2};\dfrac{1}{2}\right)\) và các hoán vị của chúng

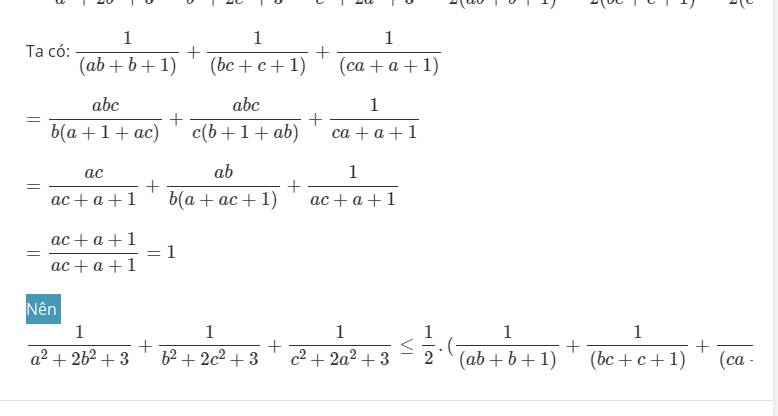

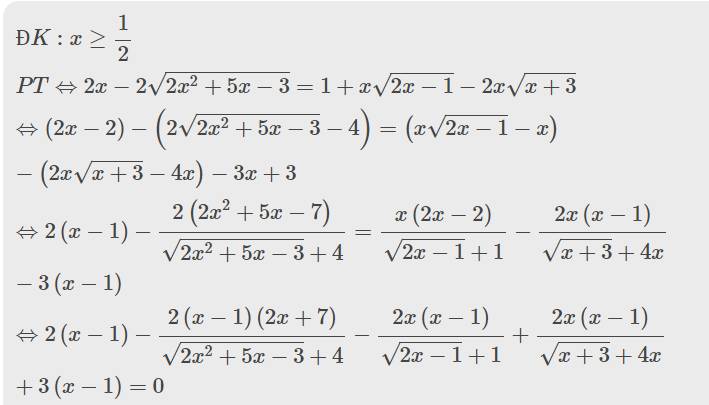

Sửa đề: a + 2b + 3c = 1
Xét: \(4x^2-4\left(2a+1\right)x+4a^2+192abc+=0\)
có: \(\Delta_1'=4\left(2a+1\right)^2-4\left(4a^2+192abc+1\right)=16a-768abc=16a\left(1-48bc\right)\)
Xét \(4x^2-4\left(2b+1\right)x+4b^2+96abc+1=0\)
có: \(\Delta_1'=4\left(2b+1\right)^2-4\left(4b^2+96abc+1\right)=16b-384abc=16b\left(1-24ac\right)\)
Ta lại xét: \(\left(1-48bc\right)+\left(1-24ac\right)=2-24c\left(a+2b\right)\)
\(=2-24c\left(1-3c\right)=2\left(36c^2-12c+1\right)=2\left(6c-1\right)^2\ge0\)với mọi c
=> Tồn tại ít nhất 1 trong 2 số: \(\left(1-48bc\right);\left(1-24ac\right)\) không âm
Vì a và b không âm
=> Tồn tại ít nhất 1 trong 2 số : \(16a\left(1-48bc\right);16b\left(1-24ac\right)\)không âm
=> Tồn tại it nhất 1 trong 2 \(\Delta_1';\Delta_2'\)không âm
=> Có ít nhất 1 trong 2 phương trình trên có nghiệm.