
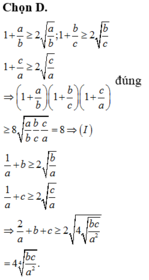
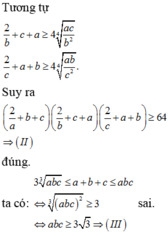
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

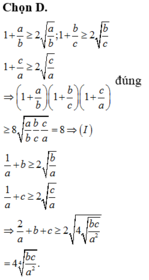
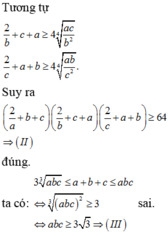

Ta có :
\(a^{\log_bc}=c^{\log_ba}\Rightarrow a^{\log_bc}+c^{\log_ab}=c^{\log_ba}+c^{\log_ab}\ge2\sqrt{c^{\log_ba}.c^{\log_ab}}=2\sqrt{c^{\log_ba+\log_ab}}\) (1)
Vì \(a,b>1\) nên áp dụng BĐT Cauchy cho 2 số không âm \(\log_ba\) và \(\log_ab\), ta được :
\(\log_ab+\log_ba\ge2\sqrt{\log_ab.\log_ba}=2\) (2)
Từ (1) và (2) \(\Rightarrow a^{\log_bc}+b^{\log_ab}\ge2\sqrt{c^2}=2c\)
hay \(\Rightarrow a^{\log_bc}+c^{\log_ab}\ge2c\)
Chứng minh tương tự ta được :
\(a^{\log_bc}+b^{\log_ca}\ge2a\)
\(b^{\log_ca}+c^{\log_ab}\ge2b\)
\(\Rightarrow2\left(a^{\log_bc}+b^{\log_ca}+c^{\log_ab}\right)\ge2\left(a+b+c\right)\)
hay :
\(a^{\log_bc}+b^{\log_ca}+c^{\log_ab}\ge a+b+c\) (*)
Mặt khác theo BĐT Cauchy ta có : \(a+b+c\ge3\sqrt[3]{abc}\) (2*)
Từ (*) và (2*) ta có :
\(a^{\log_bc}+b^{\log_ca}+c^{\log_ab}\ge3\sqrt[3]{abc}\)

Xét \(\left(a-b\right)-\left(b+c\right)+\left(c-a\right)+\left(a+b-c\right)\) ta có:
\(\left(a-b\right)-\left(b+c\right)+\left(c-a\right)+\left(a+b-c\right)\)
\(=a-b-b-c+c-a+a+b-c\)
\(=\left(a-a+a\right)-\left(b+b-b\right)-\left(c-c+c\right)\)
\(=a-b-c\) ( luôn đúng )
Vậy đẳng thức \(\left(a-b\right)-\left(b+c\right)+\left(c-a\right)+\left(a+b-c\right)=a-b-c\) luôn đúng với mọi a; b; c

Đáp án C
Mệnh đề (I) đúng.
Mệnh đề (II) sai vì log3 x2 = 2log3 x > 0 khi x > 0 nên điều kiện ∀ x ∈ ℝ \ 0 chưa đủ.
Mệnh đề (III) sai vì loga (b.c) = loga b + loga c.
Số mệnh đề đúng là 1.

Ta có :
\(\log_ab\ge\log_{a+c}\left(b+c\right)\Leftrightarrow\log_ab-1\ge\log_{a+c}\left(b+c\right)-1\)
\(\Leftrightarrow\log_a\frac{b}{a}\ge\log_{a+c}\frac{b+c}{a+c}\)
Với \(1< a\le b\) và \(c\ge0\Rightarrow\frac{b}{a}\ge\frac{b+c}{a+c}\ge1\) nên \(\log_a\frac{b}{a}\ge\log_a\frac{b+c}{a+c}\) (*)
Mặt khác, ta được : \(\log_a\frac{b+c}{a+c}\ge\log_{a+c}\frac{b+c}{a+c}\) (**)
Từ (*) và (**) \(\Rightarrow\log_ab\ge\log_{a+c}\left(b+c\right)\)
Dấu "=" xảy ra khi c = 0 hoặc a = b

Vì \(a,b>1\) và \(c\ge0\Rightarrow0< \log_ba\le\log_b\left(a+c\right)\)
\(\Rightarrow\frac{1}{\log_ba}\ge\frac{1}{\log_b\left(a+c\right)}\Leftrightarrow\log_ab\ge\log_{a+c}b\)
\(\Rightarrow\) điều phải chứng minh