Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác ABC vuông tại A có AB=3 cm; BC= 5 cm
=> AB\(^2\)+BC\(^2\)=AC\(^2\)
= 3\(^2\)+5\(^2\) =AC\(^2\)
=9 + 25= AC\(^2\)
=> 34 = AC\(^2\)
=> \(\sqrt{34}\)= AC
Vậy AC = \(\sqrt{34}\) cm
1) Áp dụng định lí Py-ta-go vào tam giác ABC:
BC2= AB2+ AC2
--> AC2= BC2 - AB2= 52 - 32= 25- 9 = 16
\(\Rightarrow\)AC = \(\sqrt{16}=4\) (cm)
2) Xét \(\Delta\)BAD và \(\Delta\)BHD :
BAD=BHD=90o
BD chung
ABD=HBD
\(\Rightarrow\) \(\Delta\)BAD = \(\Delta\)BHD (cạnh huyền_góc nhọn)
\(\Rightarrow\)BA=BH (2 cạnh t/ứng)
\(\Rightarrow\)B cách đều 2 đầu mút của đoạn AH \(\Rightarrow\) BH vuông góc với AH
3) ko biết

Mình đã đăng lại câu hỏi dễ hiểu hơn theo link này rồi ạ: https://olm.vn/hoi-dap/detail/1306671964747.html?auto=1

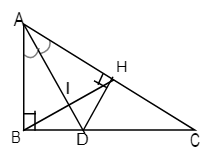
a) Xét ΔABD và ΔAHD có:
∠ABD = ∠AHD = 90 (gt)
Cạnh AD chung
∠BAD = ∠HAD (gt)
⇒ ΔABD = ΔAHD (ch - gn)
b) Xét ΔABC có:
∠B = 90o
⇒ ∠A + ∠C =90o
⇒ ∠C = 90o − ∠A = 90o − 60o = 30o
Vì AD là tia phân giác của ∠A (gt)
⇒ ∠BAD = ∠DAC = ∠A/2 = 60o/2 = 30o
⇒ ∠C = ∠DAC = 30o
⇒ ΔADC cân tại D
⇒ AD = DC
⇒ AH = HC (quan hệ giữa đường xiên và hình chiếu)
c) Xét ΔABD có :
AB < AD (cạnh góc vuông < cạnh huyền)
Mà AD = DC (cmt)
⇒ DC > AB

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔABD=ΔHBD

5 )
tự vẽ hình nha bạn
a)
Xét tam giác ABM và tam giác ACM có :
AM cạnh chung
AB = AC (gt)
BM = CM (gt)
suy ra : tam giác ABM = tam giác ACM ( c-c-c)
suy ra : góc BAM = góc CAM ( 2 góc tương ứng )
Hay AM là tia phân giác của góc A
b)
Xét tam giác ABD và tam giác ACD có :
AD cạnh chung
góc BAM = góc CAM ( c/m câu a)
AB = AC (gt)
suy ra tam giác ABD = tam giác ACD ( c-g-c)
suy ra : BD = CD ( 2 cạnh tương ứng)
C) hay tam giác BDC cân tại D