Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

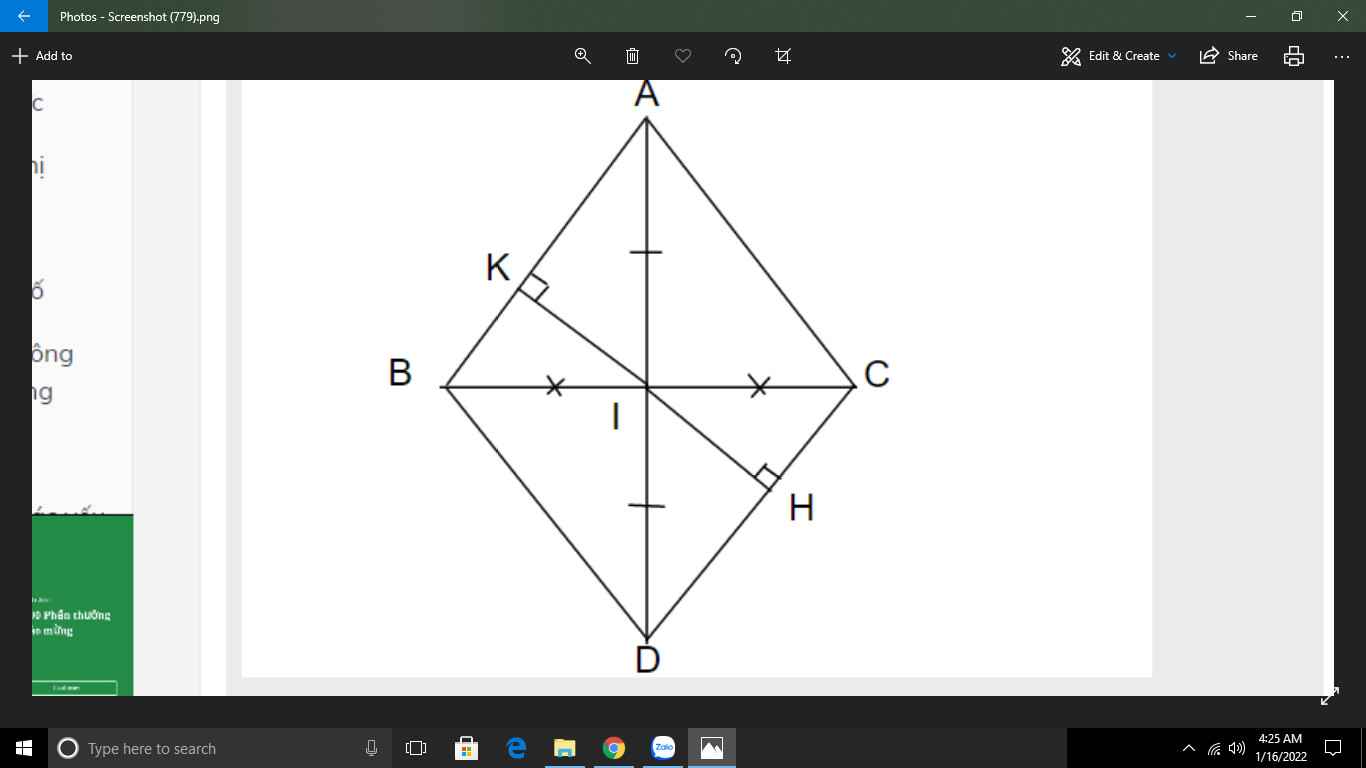
\(\text{a)}\text{Xét }\Delta ABI\text{ và }\Delta ACI\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(BI=CI\text{(I trung điểm BC)}\)
\(AI\text{ chung}\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\text{b)Xét }\Delta AIC\text{ và }\Delta DIB\text{ có:}\)
\(AI=DI\left(gt\right)\)
\(\widehat{AIC}=\widehat{DIB}\text{(đối đỉnh)}\)
\(IC=IB\)
\(\Rightarrow\Delta AIC=\Delta DIB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DIB}=\widehat{ICA}\text{(2 góc tương ứng)}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow AC=BD\)
\(\text{c)Xét }\Delta IKB\text{ và }\Delta IHC\text{ có:}\)
\(\widehat{IKB}=\widehat{IHC}=90^0\)
\(IB=IC\)
\(\widehat{KIB}=\widehat{CIH}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta IKB=\Delta IHC\left(ch-gn\right)\)
\(\Rightarrow IK=IH\)
\(\text{Hình có chỗ nào bạn ko thấy rõ thì ib riêng cho mik nghe:3}\)

Xét\(\Delta AIC\) và \(\Delta KIB\)
có: BI=IC (I là trung điểm của BC)
\(\widehat{AIC}=\widehat{BIK}\)(hai góc đối đỉnh)
AI=IK (gt)
=)\(\Delta AIC=\Delta KIB\) (c.g.c)
=)\(\widehat{CAI}=\widehat{BKI}\)(hai góc tương ứng)

a: Xét ΔAIB và ΔAIC có
AB=AC
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC
b: Ta có: ΔABC cân tại A
mà AI là đường trung tuyến
nên AI là đường cao
c: Xét tứ giác ABEC có
I là trung điểm của AE
I là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: AB//EC

A) XÉT \(\Delta BAM\)VÀ\(\Delta KCM\)CÓ
\(AM=CM\left(GT\right)\)
\(\widehat{M_1}=\widehat{M_2}\left(Đ/Đ\right)\)
\(BM=KM\left(GT\right)\)
\(\Rightarrow\Delta BAM=\Delta KCM\left(C-G-C\right)\)
\(\Rightarrow\widehat{BAM}=\widehat{KCM}=90^o\)hai góc tương ứng
HAY \(\widehat{ACK}=90^o\)
b) XÉT \(\Delta IBN\)VÀ\(\Delta CAN\)CÓ
\(IN=CN\left(GT\right)\)
\(\widehat{N_1}=\widehat{N_2}\left(Đ/Đ\right)\)
\(BN=AN\left(GT\right)\)
\(\Rightarrow\Delta IBN=\Delta CAN\left(C-G-C\right)\)
\(\Rightarrow\widehat{IBN}=\widehat{CAN}=90^o\)hai góc tương ứng
hai góc này ở vị trí SO LE TRONG BẰNG NHAU
\(\Rightarrow IB//AC\left(đpcm\right)\)
VÀ\(\widehat{BAM}=\widehat{KCM}=90^o\)
HAY\(\widehat{BAC}=\widehat{ACK}=90^o\)
HAI GÓC NÀY Ở VỊ TRÍ SO LE TRONG BẰNG NHAU
\(\Rightarrow AK//BC\left(đpcm\right)\)
C)VÌ\(\widehat{IBN}=\widehat{CAN}=90^o\)
HAY\(\widehat{IBA}=\widehat{BAC}=90^o\)
HAI GÓC NÀY Ở VỊ TRÍ SO LE TRONG BẰNG NHAU
\(\Rightarrow IA//BC\left(1\right)\)
MÀ\(AK//BC\left(CMT\right)\left(2\right)\)
TỪ (1)VÀ (2) => I,A,K THẲNG HÀNG
a) Xét \(\Delta AIBvà\Delta KICcó\)
AI=KI( giả thiết)
\(\widehat{AIB}=\widehat{KIC}\) (2 góc đối đỉnh)
IB=IC(vì I là trung điểm của BC )
\(\Rightarrow\Delta AIB=\Delta KIC\left(c-g-c\right)\)
vậy \(\Delta AIB=\Delta KIC\)
b)vậy \(\Delta AIB=\Delta KIC\)(chứng minh câu a )
\(\Rightarrow\widehat{KCI}=\widehat{ABI}\) ( 2 góc tương ứng )
hay \(\widehat{KCB}=\widehat{ABC}\) mà 2 góc này là 2 góc so le trong của đường thẳng CB cắt 2 đường thẳng CK và AB
\(\Rightarrow CK//AB\)
\(\Rightarrow\widehat{AC}K+\widehat{BAC}=180độ\) (2 góc trong cùng phía )
\(\Rightarrow\widehat{ACK}+110độ=180độ\)
\(\Rightarrow\widehat{ACK}=180độ-110độ=70độ\)
Vậy\(\widehat{ACK}=70độ\)
a) Xét \(\Delta AIBvà\Delta KICcó\)
AI=KI( giả thiết)
\(\widehat{AIB}=\widehat{KIC}\) (2 góc đối đỉnh)
IB=IC(vì I là trung điểm của BC )
\(\Rightarrow\Delta AIB=\Delta KIC\left(c-g-c\right)\)
vậy \(\Delta AIB=\Delta KIC\)
b)vậy \(\Delta AIB=\Delta KIC\)(chứng minh câu a )
\(\Rightarrow\widehat{KCI}=\widehat{ABI}\) ( 2 góc tương ứng )
hay \(\widehat{KCB}=\widehat{ABC}\) mà 2 góc này là 2 góc so le trong của đường thẳng CB cắt 2 đường thẳng CK và AB
\(\Rightarrow CK//AB\)
\(\Rightarrow\widehat{AC}K+\widehat{BAC}=180độ\) (2 góc trong cùng phía )
\(\Rightarrow\widehat{ACK}+110độ=180độ\)
\(\Rightarrow\widehat{ACK}=180độ-110độ=70độ\)
Vậy\(\widehat{ACK}=70độ\)