Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔADC có
AM vừa là đường cao vừa là phân giác
nên ΔADC cân tại A
b: Xét ΔBCD có
ME//BC
nên ME/BC=DM/DC=1/2
=>ME=4cm
Xét ΔDAC có MF//AC
nên MF/AC=DM/DC=DF/DA=1/2
=>MF=3cm
DF/DA=1/2
=>DF/(DB+4)=1/2
=>EF=DF-DE=1/2DA-1/2DB=1/2AB=1/2*2=2cm
=>C=3+4+2=9cm

ta có
góc DAE= 1/2 góc BAC ( AD là tia phân giác góc BAC)
goc FEC=1/2 góc DEC (EF là tia phân giác góc DEC)
góc BAC= góc DEC (2 góc đồng vị và AB//DE)
-> goc DAE=góc FEC
mà góc DAE và góc FEC nằm ở vị trí đồng vị
nên AD//EF
ta có
góc DAE =1/2 góc BAC (AD là tia phân giác góc BAC)
góc EAK=1/2 góc EAz ( AK là tia phân giác góc zAC)
-> góc DAE+ góc EAK= 1/2 ( góc BAC+ góc EAz)
mà góc BAC + góc EAz=180 ( 2 góc kề bù)
nên goc DAE+ góc EAK=1/2.180=90
-> goc DAK =90
-> DA vuông góc AK
lại có EK vuông góc At tai K (gt)
do dó AD//EK
ta có
AD//EK (cmt)
AD//EF(cmt)
-> EK trùng EF ( tiên đề Ơ clit)
-> E,K,F thẳng hàng

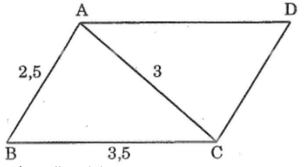
Ta có: AB // CD (gt)
Suy ra ∠(ACD) =∠(CAB) ̂(hai góc so le trong)
BC // AD (gt)
Suy ra: ∠(CAD) =∠(ACB) (hai góc so le trong)
Xét ΔABC và ΔCDA, ta có:
∠(ACB) = ∠(CAD) (chứng minh trên)
AC cạnh chung
∠(CAB) = ∠(ACD) (chứng minh trên)
Suy ra: ΔABC= ΔCDA (g.c.g)
Suy ra: CD = AB = 2,5cm và AD = BC = 3,5 cm
Chu vi ΔACD là : AC + AD + CD = 3 + 3,5 + 2,5 = 9 cm

a: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là phân giác của góc BAC
c: ΔABC cân tại A
mà AH là trung tuyến
nên AH là trung trực của BC
=>I nằm trên trung trực của BC
=>IB=IC
d: Xet ΔABN có góc ABN=góc ANB=góc MBC
nên ΔABN can tại A
=>AB=AN
e: Xét ΔABC co
BM,AM là phân giác
nên M là tâm đừog tròn nội tiếp
=>CM là phân giác của góc ACB
Xét ΔHCM vuông tại H và ΔKCM vuông tại K có
CM chung
góc HCM=góc KCM
=>ΔHCM=ΔKCM
=>MH=MK
chỉ có máy xin mới chơi đc nha cu
đúng