Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì Tam giác `ABC` cân tại A `=> AB = AC ;`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `AMB` và Tam giác `AMC` có:
`AM chung`
\(\widehat{B}=\widehat{C}\) `(CMT)`
`MB = MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `AMC (c-g-c)`
b, Vì Tam giác `AMB =` Tam giác `AMC (a)`
`=>` \(\widehat{EAM}=\widehat{FAM}\) (2 góc tương ứng).
Xét Tam giác `EAM` và Tam giác `FAM` có:
AM chung
\(\widehat{EAM}=\widehat{FAM}\) `(CMT)`
\(\widehat{AEM}=\widehat{AFM}=90^0\)
`=>` Tam giác `EAM =` Tam giác `FAM (ch-gn)`
`=> EA = FA` (2 cạnh tương ứng).
c, *câu này mình hơi bí bn ạ:')
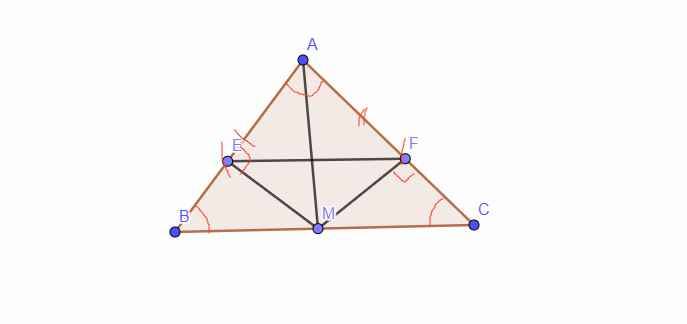
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường phân giác
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: AE=AF
Xét ΔABC có AE/AB=AF/AC
nên FE//BC

a, xét tam giác AMB và tam giác AMC có :
AB=AC (gt)
MB=MC (gt)
AM là cạnh chung
suy ra: tam giác AMB = tam giác AMC (c.c.c)
b,Vì tam giác AMB = tam giác AMC ( câu a)
suy ra : góc B =góc C ( 2 góc tương ứng )
xét tam giác MBE và tam giác MCF có:
M1=M2 ( đối đỉnh )
B =C
MB=MC ( gt)
suy ra :tam giác MBE = tam giác MCF (g.c.g)
vì tam giác MBE = tam giác MCF (chứng minh trên)
ME=MF (2 cạch tương ứng )
xét tam giác AEM và tam giác AFM có :
E1=F1
AM là cạnh chung
ME=MF
suy ra : tam giác AEM = tam giác AFM (c.g.c)
vì tam giác AEM = tam giác AFM ( chứng minh trên)
suy ra :AE=AF
c, gọi điểm cắt nhau của EF và AM
Vì tam giác AMB = tam giác AMC (câu b)
suy ra : góc A1 = góc A2 ( 2 góc tương ứng ); góc M1 = góc M2 ( 2 góc tương ứng)
xét tam giác AEH và tam giác AFH có :
A1=A2
AE=AF
AH là điểm chung
suy ra : tam giác AEH = tam giác AFH (c.g.c)
suy ra góc H1= góc H2 ( 2 góc tương ứng)
mà H1+H2=180 (2 góc kề bù)
suy ra : H1=H2=90
suy ra AM vuông góc với EF
mà M1+M2=180
suy ra M1=M2=90
suy ra AM vuông góc với BC
mà AM vuông góc với EF
suy ra EF song song với BC ( 2 đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3 thì chúng song song với nhau )
d, Ta có : AMB = NMC ( đối đỉnh )
+) AMB+AMC= 180 ( 2 góc kề bù )
mà AMC=NMC
suy ra AMB+NMC =180 (3)
mà AMB+NMC = AMN (4)
Từ (3),(4) suy ra : 3 điểm A,M,N thẳng hàng
1, xét tam giác AMB và tam giác AMC có:
AB=AC (gt)
MB=MC (gt)

vì M là trung điểm của BC\(\Rightarrow\)BM=MC
xét tam giác AMB VÀ AMC CÓ
AM CHUNG CẠNH (gt)
AB=AC(gt)
BM=MC (GT)
\(\Rightarrow\)ĐIỀU CẰN CHÚNG MINH
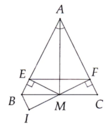
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tai F có
AM chung
góc EAM=góc FAM
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC