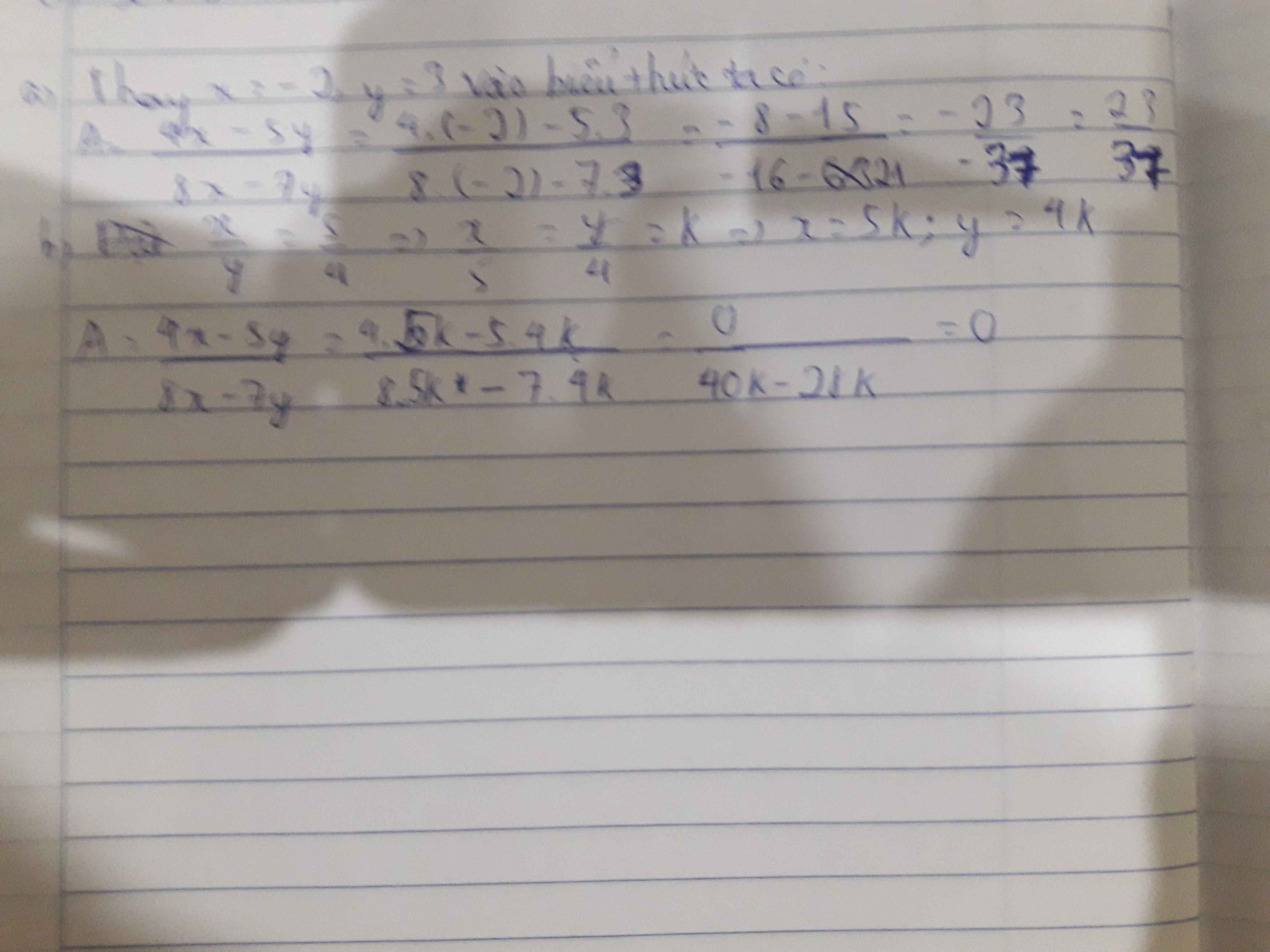DT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 3 2022
a, Thay x = -2 ; y = 3 ta được
\(A=\dfrac{4\left(-2\right)-5.3}{8\left(-2\right)-7.3}=\dfrac{-8-15}{-16-21}=\dfrac{23}{37}\)
b, Ta có \(\dfrac{x}{y}=\dfrac{5}{4}\Rightarrow\dfrac{x}{5}=\dfrac{y}{4}=k\Rightarrow x=5k;y=4k\)
Thay vào ta được \(A=\dfrac{4.5k-5.4k}{8.5k-7.4k}=\dfrac{0}{40k-28k}=0\)
1 tháng 2 2022
\(A=\dfrac{2}{3}+\dfrac{3}{4}\cdot\dfrac{-4}{9}=\dfrac{2}{3}-\dfrac{1}{3}=\dfrac{1}{3}=\dfrac{100}{300}\)
\(B=\dfrac{25}{11}\cdot\dfrac{13}{12}\cdot\dfrac{-11}{5}=\dfrac{-65}{12}=\dfrac{-1625}{300}\)
\(C=\left(\dfrac{3}{4}-\dfrac{1}{5}\right)\cdot\left(\dfrac{2}{5}-\dfrac{4}{5}\right)=\dfrac{11}{20}\cdot\dfrac{-2}{5}=\dfrac{-22}{100}=\dfrac{-11}{50}=\dfrac{-66}{300}\)
Vì -1625<-66<100
nên B<C<A
TT
3
31 tháng 8 2016
\(\text{Ta có: |a| = }\frac{1}{3}\Leftrightarrow a=\orbr{\begin{cases}\frac{1}{3}\\-\frac{1}{3}\end{cases}}\)
\(\text{Ta có: |b| = }0,25\Leftrightarrow b=\orbr{\begin{cases}0,25\\-0.25\end{cases}}\)
Thay a. b vào ta có:
A =
HN
2
H
0
28 tháng 6 2015
1) \(\left|2x+5\right|\ge21\Rightarrow2x+5\ge21\)hoặc \(2x+5
28 tháng 6 2015
2b) Áp dụng bất đẳng thức giá trị tuyệt đối: |a| + |b| \(\ge\) |a + b|. Dấu "=" xảy ra khi tích a.b \(\ge\) 0
Ta có: B = |2x - 1| + |3 - 2x| + 5 \(\ge\) |2x - 1+3 - 2x| + 5 = |2| + 5 = 7
=> Min B = 7 khi
(2x - 1)( 3 - 2x) \(\ge\) 0 => (2x - 1)(2x - 3) \(\le\) 0
Mà 2x - 1 > 2x - 3 nên 2x - 1 \(\ge\) 0 và 2x - 3 \(\le\) 0
=> x \(\ge\) 1/2 và x \(\le\) 3/2
LT
1
16 tháng 3 2021
a) Thay x = 3,y = 4 vào biểu thức P = 2x + 3y - 1 ta có :
P = 2x + 3y - 1 = 2.3 + 3.4 - 1 = 6 + 12 - 1 = 17
Vậy P = 17
b) Thay x = -3,y = -1 vào biểu thức P = 2x + 3y - 1 ta có :
P = 2x + 3y - 1 = 2(-3) + 3(-1) - 1 = -10
Vậy P = -10
c) x = y = -1/2 thì :
P = 2x + 3y - 1 = \(2\cdot\left(-\frac{1}{2}\right)+3\cdot\left(-\frac{1}{2}\right)-1=5\left(-\frac{1}{2}\right)-1=-\frac{5}{2}-\frac{2}{2}=-\frac{7}{2}\)
Vậy P = -7/2
