Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có = (2; -5). Gọi M(x; y) là 1 điểm nằm trên đường thẳng AB thì AM = (x - 1; y - 4). Ba điểm A, B, M thẳng hàng nên hai vec tơ
và
cùng phương, cho ta:
=
<=> 5x + 2y -13 = 0
Đó chính là phương trình đường thẳng AB.
Tương tự ta có phương trình đường thẳng BC: x - y -4 = 0
phương trình đường thẳng CA: 2x + 5y -22 = 0
b) Đường cao AH là đường thẳng đi qua A(1; 4) và vuông góc với BC.
= (3; 3) =>
⊥
nên
nhận vectơ
= (3; 3) làm vectơ pháp tuyến và có phương trình tổng quát:
AH : 3(x - 1) + 3(y -4) = 0
3x + 3y - 15 = 0
=> x + y - 5 = 0
Gọi M là trung điểm BC ta có M \(\left(\dfrac{9}{2};\dfrac{1}{2}\right)\)
Trung tuyến AM là đường thẳng đi qua hai điểm A, M. Theo các viết phương trình đường thẳng đi qua hai điểm trong câu a) ta viết được:
AM : x + y - 5 = 0

Đường tròn tâm O(a,b)
\(\Delta_1\) đi qua \(AB..\Delta_1:\left(x-1\right)-\left(y-2\right)=x-y+1=0\)
\(\Delta_2\) trung trực AB: \(\Delta_2:\left(x-2\right)+\left(y-3\right)=x+y-5=0\)
Tâm (c) phải thuộc \(\Delta_2\) =>O(a,5-a)
Gọi I là điểm tiếp xúc \(\Delta\) và (C) ta có hệ pt
\(\Rightarrow\left\{{}\begin{matrix}OA=OB=\sqrt{\left(a-1\right)^2+\left(5-a-3\right)^2}=R\\OI=\left|3a+\left(5-a\right)-3\right|=\sqrt{10}R\end{matrix}\right.\)
\(\left\{{}\begin{matrix}a^2-2a+1+a^2-4a+4=R^2\\\left(2a+2\right)^2=10R^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2a^2-6a+5=R^2\\4a^2+8a+4=10R^2\end{matrix}\right.\)
Lấy [(1) nhân 5] trừ [(2) chia 2]
\(\Leftrightarrow8a^2-32a+23=0\left\{\Delta=16^2-8.23=8.32-8.23=8\left(32-23\right)=2.4.9\right\}\) đề số lẻ thế nhỉ
\(\Rightarrow a=\left[{}\begin{matrix}\dfrac{16-6\sqrt{2}}{8}=2-\dfrac{3\sqrt{2}}{4}\\\dfrac{16+6\sqrt{2}}{8}=2+\dfrac{3\sqrt{2}}{4}\end{matrix}\right.\)
\(\Rightarrow b=\left[{}\begin{matrix}3+\dfrac{3\sqrt{2}}{4}\\3-\dfrac{3\sqrt{2}}{4}\end{matrix}\right.\) \(\Rightarrow R^2=\left[{}\begin{matrix}\dfrac{\left(6-\dfrac{3\sqrt{2}}{2}\right)^2}{10}\\\dfrac{\left(6+\dfrac{3\sqrt{2}}{2}\right)^2}{10}\end{matrix}\right.\)
(C) =(x-2+3sqrt(2)/4)^2 +(y-3-3sqrt(2)/4)^2 =(6-3sqrt(2)/2)^2/10

\(\overrightarrow{AB}=\left(-3;4\right)\Rightarrow\) đường thẳng AB nhận \(\left(4;3\right)\) là 1 vtpt
Phương trình AB:
\(4\left(x-3\right)+3\left(y-1\right)=0\Leftrightarrow4x+3y-15=0\)
b.
\(R=d\left(C;AB\right)=\dfrac{\left|4.6+1.3-15\right|}{\sqrt{4^3+3^2}}=\dfrac{12}{5}\)
Phương trình (C):
\(\left(x-6\right)^2+\left(y-1\right)^2=\dfrac{144}{25}\)

Đường thẳng Δ song song với d ⇒ Δ: x + y + c = 0, (c ≠ 0)
Vì Δ đi qua A ⇒ 3 + 0 + c = 0 ⇒ c = -3(tm)
Vậy đường thẳng Δ có dạng: x+y-3=0
Vì đường tròn có tâm I thuộc d nên I(a;-a)
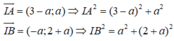
Vì đường tròn đi qua A, B nên I A 2 = I B 2 ⇒ (3 - a ) 2 + a 2 = a 2 + (2 + a ) 2 ⇔ (3 - a ) 2 = (2 + a ) 2
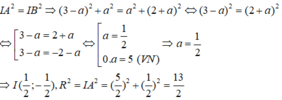
Vậy phương trình đường tròn có dạng:
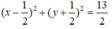
Ta có:
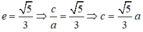
Giả sử elip (E) có dạng:
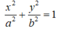
Vì (E) đi qua B nên:
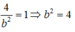
Mà
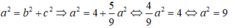
Vậy phương trình chính tắc của elip (E) là:
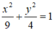

a: Vì Δ//d nên Δ: 3x-4y+c=0
Thay x=1 và y=4 vào Δ, ta được:
c+3-16=0
=>c=13
b: Vì Δ vuông góc d nên Δ: 4x+3y+c=0
Thay x=-3 và y=-5 vào Δ, ta được:
c+4*(-3)+3(-5)=0
=>c-27=0
=>c=27
=>4x+3y+27=0

a.
\(\overrightarrow{BC}=\left(2;-3\right)\Rightarrow\) đường thẳng BC nhận (3;2) là 1 vtpt
Phương trình BC:
\(3\left(x-2\right)+2\left(y-3\right)=0\Leftrightarrow3x+2y-12=0\)
b.
Gọi G là trọng tâm ABC \(\Rightarrow G\left(\dfrac{7}{3};\dfrac{4}{3}\right)\)
(C) tiếp xúc BC \(\Leftrightarrow d\left(G;BC\right)=R\)
\(\Rightarrow R=\dfrac{\left|3.\dfrac{7}{3}+2.\dfrac{4}{3}-12\right|}{\sqrt{3^2+2^2}}=\dfrac{7\sqrt{13}}{39}\)
Phương trình: \(\left(x-\dfrac{7}{3}\right)^2+\left(y-\dfrac{4}{3}\right)^2=\dfrac{49}{117}\)