Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi \(M\left(m;2m-3\right)\)
C1:
Khi đó \(\overrightarrow{MA}=\left(-m;-2m\right)\) và \(\overrightarrow{BM}=\left(m-1;2m-6\right)\)
Ta có \(AM+MB=\left|\overrightarrow{MA}\right|+\left|\overrightarrow{BM}\right|\)\(\ge\left|\overrightarrow{MA}+\overrightarrow{BM}\right|\)\(=\sqrt{\left(-m+m-1\right)^2+\left(-2m+2m-6\right)^2}\)\(=\sqrt{37}\)
Đẳng thức xảy ra\(\Leftrightarrow m=0\)
Khi đó, \(M\left(0;-3\right)\)
C2:
Áp dụng BĐT tam giác mở rộng, ta có
\(AM+MB\ge AB=\sqrt{37}\)
Giải ra cũng tìm được \(M\left(0;-3\right)\) thoả mãn

Đáp án D
Do M thuộc d nên M( x; 2x+ 3)
Suy ra:
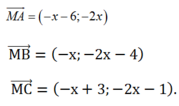
Do đó:
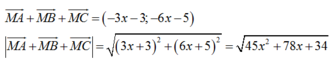
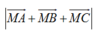
nhỏ nhất khi và chỉ khi: f(x) = 45x2+ 78x + 34 nhỏ nhất
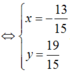

Ta thấy \(\left(2-2+1\right)\left(1-0+1\right)=2>0\Rightarrow A,B\) khác phía so với \(\Delta\)
Lấy B' đối xứng với B qua \(\Delta\)
BB' có phương trình \(2x+y+m=0\)
Do B thuộc đường thẳng BB' nên \(m=-2\Rightarrow BB':2x+y-2=0\)
B' có tọa độ là nghiệm của hệ \(\left\{{}\begin{matrix}x-2y+1=0\\2x+y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{5}\\y=\dfrac{4}{5}\end{matrix}\right.\Rightarrow B'=\left(\dfrac{3}{5};\dfrac{4}{5}\right)\)
a, \(MA+MB=MA+MB'\ge AB'\)
\(min=AB'\Leftrightarrow M\) là giao điểm của AB' và \(\Delta\)
\(\Leftrightarrow...\)
b, \(\left|MA-MB\right|=\left|MA-MB'\right|\le AB'\)
\(max=AB'\Leftrightarrow M\) là giao điểm của AB' và \(\Delta\)
\(\Leftrightarrow...\)

a: Δ//d
=>Δ: 2x-y+c=0
Thay x=1 và y=-2 vào Δ, ta được:
c+2+2=0
=>c=-4
b: B thuộc d nên B(x;2x+3)
M(1;-2); A(0;3)
\(\overrightarrow{MA}=\left(-1;5\right);\overrightarrow{MB}=\left(x-1;2x+5\right)\)
ΔBAM vuông tại M
=>-1(x-1)+5(2x+5)=0
=>-x+1+10x+25=0
=>9x=-26
=>x=-26/9
=>B(-26/9;-25/9)

Thay tọa độ A và B vào d thấy kết quả cùng dấu \(\Rightarrow\) A và B nằm cùng phía so với d
Gọi C là điểm đối xứng A qua d \(\Rightarrow MA=CM\Rightarrow MA+MB=CM+MB\ge CB\)
\(\Rightarrow MA+MB\) nhỏ nhất khi M;B;C thẳng hàng hay M là giao điểm của đường thẳng BC và d
Phương trình d' qua A và vuông góc d có dạng:
\(1\left(x-1\right)+2\left(y-0\right)=0\Leftrightarrow x+2y-1=0\)
D là giao điểm d và d' \(\Rightarrow\left\{{}\begin{matrix}x+2y-1=0\\2x-y+3=0\end{matrix}\right.\) \(\Rightarrow D\left(-1;1\right)\)
C đối xứng A qua d khi và chỉ khi D là trung điểm AC \(\Rightarrow C\left(-3;1\right)\)
\(\Rightarrow\overrightarrow{CB}=\left(5;0\right)=5\left(1;0\right)\Rightarrow\) phương trình BC có dạng:
\(0\left(x-2\right)+1\left(y-1\right)=0\Leftrightarrow y-1=0\)
M là giao điểm d và BC nên tọa độ thỏa mãn: \(\left\{{}\begin{matrix}y-1=0\\2x-y+3=0\end{matrix}\right.\) \(\Rightarrow M\left(-\frac{3}{2};1\right)\)
A,B cùng phía so với d.
Gọi A' là điểm đối xứng của A qua d
MA+MB=MA'+MB>=A'B
Dấu = xảy ra khi A',M,B thẳng hàng
=>M là giao của A'B với d
Gọi d' là đường đi qua A và vuông góc d
d: 2x-y-3=0
=>d': x+2y+c=0
Thay x=0 và y=-3 vào (d'),ta được:
0+2*(-3)+c=0
=>c=6
=>d': x+2y+6=0
Gọi H là giao của d' và d
Tọa độ H là:
x+2y=-6 và 2x-y=3
=>x=0 và y=-3
H là trung điểm của AA' nên ta có:
0+x=0 và y-3=-6
=>x=0 và y=-3
=>A'(0;-3)
mà B(1;3) nên A'B có VTPT là (-6;1)
Phương trình A'B là:
-6(x-1)+1(y-3)=0
=>-6x+6+y-3=0
=>-6x+y+3=0
Tọa độ M là:
-6x+y=-3 và 2x-y=3
=>x=0 và y=-3